共轭的那些事儿

南箕北有斗,牵牛不负轭。——汉·《明月皎夜光》
一、引言
在没有深挖这个词之前,只是一直觉得它听起来既优雅又神秘。直到最近看一些Paper,里面涉及到了共轭梯度,再想起之前学过的共轭曲线、共轭复数、共轭转置,忽然觉得这些花狸狐哨的名词背后可能隐藏者一个不被我所知的理论体系,出于好奇和知识回顾的需要,就有了这篇文章。
1.1 轭及共轭
轭这个词汉语里面是有的,但是共轭(conjugate/conjugation)这个词(概念)却是从英语里面翻译过来的。与熵(entropy)这类词所不同的是,轭这个词是有真真切切的实物所对应的,是有非常具象的含义而非译者自己凭空创造出来的。下面这个图就是一副轭:

上图实际上是一副牛轭,分别将两只牛的牛头塞进那两个木套子,就能驭使它们犁地、耕田、拉货。如果只有一个套子的,就只能驭使一头牛,即为单轭。像上面这样有两个套子的,即为双轭(共轭)。
1.2 共轭关系
有了图就很好解释和理解了。所谓的共轭关系是什么关系?共轭关系就是这幅双轭里面两头牛之间的关系:既相互制衡,相互约束,相互对立,又相互支撑,相互依存,相互统一。由于科学技术的长足发展,许多原本统一的概念在各个领域有了自己专属的含义。共轭也一样,在不同的科学领域有着不同的定义,共轭这个术语出现的学科包括但不限于以下这些:
- 1. 数学;
- 2. 化学;
- 3. 物理;
本文主要还是针对其数学领域而言,其他领域的请自行参考相关资料。
二、共轭(数学)
2.1 共轭的类型
目前数学里面定义的共轭的类型包括但不限于以下内容:
- 1. 共轭复数;
- 2. 共轭根式;
- 3. 共轭元素(场论);
- 4. 谐波共轭;
- 5. 共轭转置;
- 6. 共轭梯度法;
- 7. 共轭先验/分布;
- 8. 共轭线图(图论);
- 9. 共轭闭合(群论);
- 10. 等角共轭;
- 11. 共轭点;
上述定义还不是数学里面全部的概念,零零总总加起来也已经有十几个了。这也正好验证了我们最开始的猜想:共轭的背后其实有一个庞大的家族,分布在各个研究方向中。
要把这些概念都介绍一遍是非常耗时耗力的,也没有必要(其实是不了解),有许多高深的理论比如群论暂时我也用不上。因此只选择一些平时用的比较多的来讲,后面有需要的时候再来补充。
2.2 共轭复数
2.2.1 共轭复数的定义
共轭复数(复共轭)是指实数部分相等,虚数部分互为相反数的一对复数,形如:
$$
z = a + bj \stackrel{conj}{\longleftrightarrow} \bar{z} = a -bj
\tag{2 - 1}
$$
或者用极坐标的形式表示为:
$$
z = r \cdot e^{\varphi \cdot j} \stackrel{conj}{\longleftrightarrow} \bar{z} = r \cdot e^{-\varphi \cdot j}
\tag{2 - 2 - 1}
$$
上述两种形式通过欧拉公式相互连接起来,如下图所示:
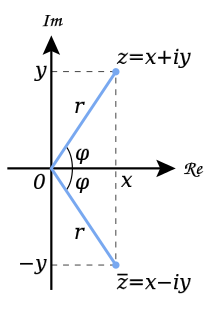
注:对于任意复数z,其共轭复数通常记作$\overline{z}$,也有的资料记作$z^*$。
2.2.2 共轭复数的性质
对任意给定的两复数$z、w$,有:
$$
\begin{cases}
\begin{split}
\overline{z \pm w} &= \overline{z} \pm \overline{w} \\
\overline{\lgroup \frac{z}{w} \rgroup} &= \frac{\overline{z}}{\overline{w}}, w \neq 0 \\
\overline{z \ast w} &= \overline{z} \ast \overline{w} \\
\overline{z^n}&= (\overline{z})^n \\
|\overline{z}| &= |z| \\
e^\overline{z} &= \overline{e^z} \\
log(\overline{z}) &= \overline{log(z)}, z \neq 0
\end{split}
\end{cases}
\tag{2 - 2 - 3}
$$
此外,对任意给定的函数\varphi(x),若它为一个全纯函数(Holomorphic function),则恒有:
$$
\varphi(\overline{z}) = \overline{\varphi(z)}
\tag{2 - 2 - 4}
$$
2.3 共轭根式
2.3.1 共轭根式的定义
共轭根式(Conjugate-squre-roots)可能是这里面最简单的了,它是指满足如下形式的一对含根号的式子:
$$
a + b \sqrt{d} \stackrel{conj}{\longleftrightarrow} a - b \sqrt{d}
\tag{2 - 3 - 1}
$$
实际上共轭复数是共轭根式的一个特例($a = 0, \ b=1, \ d=-1$)。
2.3.2 共轭根式的特性
共轭根式的主要特性是:其和、积不包含平方根项,如下所示:
$$
\begin{cases}
\begin{split}
(a + b \sqrt{d}) \cdot (a - b \sqrt{d}) &= a^2 - db^2 \\
(a + b \sqrt{d}) + (a + b \sqrt{d}) &= 2a
\end{split}
\end{cases}
\tag{2 - 3 - 2}
$$
通常我们会用共轭根式的这个特性来消除分母中的平方根,如下示例:
$$
\frac{1}{a + b \sqrt{d}} = \frac{a - b \sqrt{d}}{a^2 - db^2}
\tag{2 - 3- 3}
$$
这个技巧相信大家平时几乎都用的炉火纯青了。这里需要提醒的是,对于$d$的取值,并没有特殊要求,它甚至可以是一个复数。
2.4 共轭转置
2.4.1 共轭转置的定义
共轭转置(也称埃尔米特共轭、埃尔米特转置)定义为满足如下等式的复数矩阵:
$$
(\textbf{A}^*)_{ij} = \overline{\textbf{A}_{ji}}
\tag{2 - 4 - 1}
$$
式中矩阵$\textbf{A}^*$即表示矩阵$\textbf{A}$的共轭转置矩阵。不同的学科中有不同的记法,但都表示同一个意思。线性代数中通常用$\textbf{A}^*$或者$\textbf{A}^H$来表示。
注:按照Wikipedia的说法,某些情况下$\textbf{A}^*$仅仅表示对原矩阵$\textbf{A}$的元素取复共轭(而不做转置)后形成的矩阵,具体属于哪种情况请结合上下文判断。
上式等价的语言定义就是:共轭转置矩阵的每一个元素是原矩阵先做转置后对应元素的复共轭。共轭转置矩阵就是原矩阵先取转置矩阵,再将转置后的矩阵的每一个元素取复共轭后形成的矩阵。
也即上述定义可以等价的表示为如下等式:
$$
\textbf{A}^* = (\overline{\textbf{A}})^T = \overline{\textbf{A}^T}
\tag{2 - 4 - 2}
$$
从上式也可以看出,无论是先对原矩阵做转置,再取复共轭。还是先对原矩阵取复共轭,再做转置。最终的结果都相同。
2.4.2共轭转置的示例
共轭转置稍微复杂一些,因此我们举个例子来说明,给定如下复数矩阵:
$$
\textbf{A} =
\begin{bmatrix}
1+j & -2 & 3-2j \\
5 & 5-j & 2+j\\
-j & 4 & 3+j
\end{bmatrix}
\tag{2 - 4 - 3}
$$
则其对应的共轭转置为:
$$
\textbf{A}^* =
\begin{bmatrix}
1-j & 5 & j \\
-2 & 5+j & 4\\
3+2j & 2-j & 3-j
\end{bmatrix}
\tag{2 - 4 - 4}
$$
由上可知,对称矩阵实际上是共轭转置矩阵的一种特殊情况(原矩阵所有元素均为实数)。
2.4.3 共轭转置的性质
共轭转置有如下运算特性:
$$
\begin{cases}
\begin{split}
(\textbf{A} + \textbf{B})^* &= \textbf{A}^* + \textbf{B}^* \\
(r\textbf{A})^* &= \overline{r} \textbf{A}^*, \quad r为任意复数 \\
(\textbf{A} \textbf{B})^* &= \textbf{B}^* \textbf{A}^* \\
(\textbf{A}^*)^* &= \textbf{A} \\
det(\textbf{A}^*) &= (det \ \textbf{A})^*, \quad \text{A}为方阵 \\
tr(\textbf{A}^*) &= (tr \ \textbf{A})^*, \quad \text{A}为方阵 \\
eig(\textbf{A}^*) &= \overline{(eig \ \textbf{A})} \\
\langle \textbf{A} \vec x, \vec y \rangle &= \langle x, \textbf{A}^* \vec y \rangle \\
\end{split}
\end{cases}
\tag{2 - 4 - 5}
$$
上式中涉及矩阵乘法、矩阵与向量乘法的地方默认满足维度关系,不赘述。
2.4.4 共轭转置的延伸
如果矩阵$\textbf{A}$是一个方阵,并且其共轭转置矩阵与其自身之间满足一些特定条件,我们就给A一些特殊的称谓。
2.4.4.1 埃尔米特矩阵
如果矩阵$\textbf{A}$与其共轭转置满足如下关系:
$$
\textbf{A} = \textbf{A}^* \quad or \quad a_{ij} = \overline{a_{ji}}
\tag{2 - 4 - 6}
$$
我们就称矩阵$\textbf{A}$为埃尔米特(Hermitian)矩阵(或自伴随矩阵(self-adjoint))。
2.4.4.2 斜埃尔米特矩阵
如果矩阵$\textbf{A}$与其共轭转置满足如下关系:
$$
\textbf{A} = -\textbf{A}^* \quad or \quad a_{ij} = -\overline{a_{ji}}
\tag{2 - 4 - 7}
$$
我们就称矩阵$\textbf{A}$为斜埃尔米特(skew Hermitian)矩阵(或反埃尔米特矩阵(antihermitian))。
2.4.4.3 正规矩阵
如果矩阵$\textbf{A}$与其共轭转置满足如下关系:
$$
\textbf{A} \textbf{A}^* = \textbf{A}^* \textbf{A}
\tag{2 - 4 - 8}
$$
我们就称矩阵$\textbf{A}$为正规(normal)矩阵。
2.4.4.4 酉矩阵
如果矩阵$\textbf{A}$与其共轭转置满足如下关系:
$$
\textbf{A}^* = \textbf{A}^{-1}
\tag{2 - 4 - 9}
$$
即矩阵的共轭转置为其逆矩阵,我们就称矩阵$\textbf{A}$为酉(unitary)矩阵。
2.5 共轭先验/分布
2.5.1 共轭先验/分布的定义
根据Wikipedia的定义,在贝叶斯概率论中,如果后验概率(poeterior distributions)的概率分布$p(\theta | x)$与其对应的先验概率(prior probability)的概率分布$p(\theta)$属于相同类型的概率分布,则这对先验/后验概率分布被称为共轭分布。
此时,这个先验分布$p(\theta)$就称为似然函数(likelihood function)$p(x|\theta)$的共轭先验。共轭先验一定是相对于似然函数而言的。
这里再对先验概率、后验概率、似然函数做一个说明。
- 1. $p(\theta|x)$:后验概率,是指在给定(已知)数据(样本)$x$的情况下,模型参数为$\theta$的概率;
- 2. $p(x|\theta)$:似然函数,刚好与后验概率相反,是指在给定(已知)模型参数$\theta$的情况下,获得(观测到)数据$x$的概率;
- 3. $p(\theta)$:先验概率,是指我们在获得(观测到)任何数据(样本)之前,预先对模型参数的一个估计(经验值),比如模型属于什么类型的概率分布。
注:只有共轭分布、共轭先验的说法,并没有共轭后验这个术语。
2.5.2 常见的共轭分布
按照似然函数分布的类型,我们有如下常见的共轭分布表:
2.5.2.1 离散分布
表 2 - 1 常见离散共轭分布函数表
| 似然函数 | 共轭先验 | 模型参数 | 先验超参数 | 参数注释 |
|---|---|---|---|---|
| 伯努力分布 | Beta分布 | $p$ | $\alpha, \ \beta$ | $\alpha$、$\beta$的详细解释见这里 |
| 二项分布 | Beta分布 | 同上 | 同上 | 同上 |
| 几何分布 | Beta分布 | $p_0$ | 同上 | 同上 |
| 超几何分布 | Beta-二项分布 | $M$ | $N, \ \alpha, \ \beta$ | $\alpha, \ \beta$同上 $M$——抽样数 $N$——样本总数 |
| 泊松分布 | Gamma分布 | $\lambda$ | $k, \ \theta $ $or$ $\alpha, \ \beta$ |
$\frac{1}{\theta}(\beta)$——时间间隔 $k(\alpha)$——间隔内总次数 |
| 多项分布 | Dirichlet分布 | $p$——概率向量 $k$——概率向量维度 |
$\alpha$ | $\alpha_i$——第i个元素发生次数 |
2.5.2.2 连续分布
表 2 - 2 常见连续共轭分布函数表
| 似然函数 | 共轭先验 | 模型参数 | 先验超参数 | 参数注释 |
|---|---|---|---|---|
| 正态分布 (已知$\tau$) |
正态分布 | $\mu$ | $\mu_0, \ \sigma^2_0$ | $\mu_0$——样本均值 $\sigma^2_0$——样本方差 |
| 正态分布 (已知$\tau$) |
同上 | 同上 | $\mu_0, \ \tau_0(\frac{1}{\sigma^2_0})$ | $\mu_0$——同上 $\tau_0$——准确率 |
| 正态分布 (已知$\mu$) |
逆Gamma分布 | $\sigma^2_0$ | $\alpha, \ \beta$ | $\sigma_0 = 2\beta$ |
| 正态分布 (已知$\mu$) |
Gamma分布 | $\tau$ | $\alpha, \ \beta$ | 同上 |
| 多元正态分布 (已知$\sum$) |
多元正态分布 | $\vec \mu$ | $\vec \mu_0, \ \vec \sum_0$ | $\vec \mu_0$——样本均值向量 $\vec \sum_0$——样本协方差阵 |
| 指数分布 | Gamma分布 | $\lambda$ | $\alpha, \ \beta$ | $\alpha$、$\beta$的详细解释见这里 |
注:如果似然函数为指数函数,则其共轭先验必然存在,且通常也属于指数函数。
2.5.3 共轭分布示例
举个实际的例子可能更容易理解。我们想了解某个大学的男女生比例,于是随机在校园里面进行了抽样,在遇到的100个学生里面,发现有66个是男生。问:该学校男生的比例?
从频率学派的观点来看,有:
$$
\theta(p_{boy}) = \frac{66}{100} = 0.66
\tag{2 - 5 - 1}
$$
从频率学派的角度来看,这个(概率)值存在唯一真值,这个值是不会变化的。频率派的谬误之处在于,假设该校总共有1000人,我抽了其中800人,恰好800人全是男生,于是该校的男生比例就是100%?
从贝叶斯学派的角度出发,这个值$\theta$本身属于某个概率分布,还需要结合我们的先验知识(比如往年的统计数据、学校是文科还是理科多等等)来进行修正,确定一个合理的数据。
为了方便叙述,有如下定义:
- $m$——抽样中男生的人数;
- $N$——抽样的总人数(样本总数);
- $\theta$——在该高校中,男生比例;
- $p(\theta)$——在该高校中,男生比例$\theta$的概率分布(先验概率);
- $\textbf{X}$——在该高校中,随机抽取$N$个学生,其中有$m$个是男生的事件。
根据贝叶斯公式:
$$
\underbrace{P(\theta|\textbf{X})}_{后验概率} = \frac{\underbrace{P(\textbf{X}|\theta)}_{似然函数} \cdot \underbrace{P(\theta)}_{先验概率}} {\underbrace{P(\textbf{X})}_{边缘概率}}
\tag{2 - 5 - 2}
$$
由上式可知,在获得了学生数据(观测样本)的情况下,我们要去推断该高校的男生的比例(即后验概率$P(\theta|\textbf{X})$),需要知道三个值:似然函数、先验概率(分布)、边缘概率。
边缘概率可以视作归一化因子,那么后验概率最终就只取决于似然函数和先验概率的形式。这个例子的似然函数实际上是二项分布(每次实验只有男生、女生两种结果,)。
由此有似然函数的表达式:
$$
P(\textbf{X}|\theta) = C^m_N \theta^m \ (1 - \theta)^{N - m}
\tag{2 - 5 - 3}
$$
查离散表2-1可知,当似然函数为二项分布时,其对应的共轭先验是Beta分布。即如果我们将共轭先验选择为Beta分布,最终可以推导出后验概率也为Beta分布。
因为$\theta \sim Beta(\alpha, \ \beta)$,由此有似然函数表达式:
$$
\begin{split}
P(\theta) = P(\theta;\alpha, \ \beta) &= Beta(\alpha, \ \beta) \\
&= \frac{\theta^{\alpha - 1}(1 - \theta)^{\beta - 1}}{\Large{\int_{0}^{1}} \normalsize{u^{\alpha - 1}(1 - u)^{\beta - 1}d_u}} \\
&= \frac{\theta^{\alpha - 1}(1 - \theta)^{\beta - 1}}{B(\alpha, \ \beta)}
\end{split}
\tag{2 - 5 - 4}
$$
式中:$B(\alpha, \ \beta) = \int_{0}^{1} u^{\alpha - 1}(1 - u)^{\beta - 1}d_u = \frac{\Gamma(\alpha) \cdot \Gamma(\beta)} {\Gamma(\alpha + \beta)}$,$\Gamma(x)$为伽玛函数。
由于先验分布为连续函数,因此有边缘概率的积分表达式(如果是离散函数则为累积求和表达式):
$$
\begin{split}
P(\textbf{X}) &= \int_{0}^{1} p(\textbf{X}|\theta) p(\theta) d_{\theta} \\
&= \int_{0}^{1} C^m_N \theta^m \ (1 - \theta)^{N - m} \cdot \frac{\theta^{\alpha - 1}(1 - \theta)^{\beta - 1}} {B(\alpha, \ \beta)} \\
&= \frac{C^m_N}{B(\alpha, \ \beta)} \int_{0}^{1} \theta^{\alpha + m - 1}(1 - \theta)^{\beta + N - m - 1} \\
&= \frac{C^m_N}{B(\alpha, \ \beta)} \cdot B(\alpha + m, \ \beta + N -m)
\end{split}
\tag{2 - 5 - 5}
$$
将上述式子2-5-3、2-5-4、2-5-5代入式2-5-2有:
$$
\require{cancel}
\begin{split}
P(\theta|\textbf{X}) &= \frac{C^m_N \theta^m \ (1 - \theta)^{N - m} \cdot \frac{\theta^{\alpha - 1}(1 - \theta)^{\beta - 1}}{B(\alpha, \ \beta)}}{\frac{C^m_N}{B(\alpha, \ \beta)} \cdot B(\alpha + m, \ \beta + N -m)} \\
&= \frac{\bcancel{C^m_N} \theta^m \ (1 - \theta)^{N - m} \cdot \theta^{\alpha - 1}(1 - \theta)^{\beta - 1} \cdot \bcancel{B(\alpha, \ \beta)}}{\bcancel{C^m_N} \cdot B(\alpha + m, \ \beta + N -m) \cdot \bcancel{B(\alpha, \ \beta)}} \\
&= \frac{\theta^{\alpha + m - 1}(1 - \theta)^{\beta + N - m - 1}} {B(\alpha + m, \ \beta + N -m)} \\
\\
&= Beta(\alpha + m, \ \beta + N -m)
\end{split}
\tag{2 - 5 - 6}
$$
我们算出来的后验概率$P(\theta|\textbf{X}) \sim Beta(\alpha + m, \ \beta + N -m)$,即后验概率仍然服从$Beta$分布!
以这个题为例,假设我们抽样的高校是一个综合性大学,男女比例比较接近,由如下的$Beta$分布的概率密度函数图:
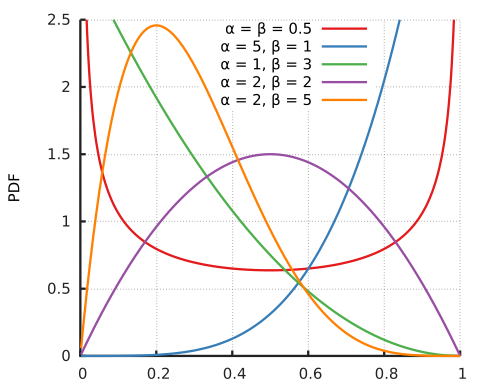
由上图推出$\alpha=2, \ \beta=2$(图中紫色曲线)比较合理,即$\theta \sim Beta(2, \ 2)$,再结合$N=100, \ m=66$可知后验概率$P(\theta|\textbf{X}) \sim Beta(68, 46)$,如下图所示:
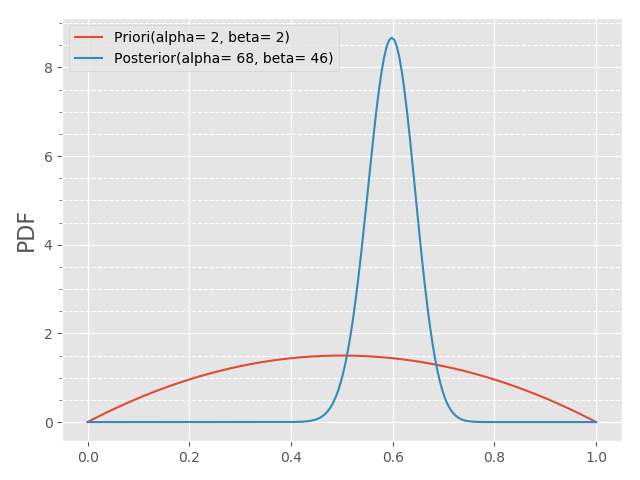
由上图可知,由于观测数据的加入,原本我们估计的男女比例均衡变成了男生比例偏高。这更符合我们的预期,模型参数会根据观测数据的变化而动态调整,同时结合了已有经验。
表中剩下的共轭分布感兴趣的可以自己验证。共轭分布最大的优点就是,后验概率会保持与先验概率相同的分布形式。
