Talk is cheap, explain me the Paper.

一、引言

  设计深度学习模型的时候，不管是自己从头搭建还是修改别人的，都离不开相关参数的计算，主要是输入图形先后经过卷积、池化层后输出尺寸的变化，尤其是涉及多个卷积或池化层时，如果对这两种操作的原理不清楚，就会对网络的各个参数产生困惑，不知道如何去修改以便适配自己的业务场景。
  这里对CNN（卷积神经网络）中的主要参数的计算做一个归纳整理，方便参考。我们先用图示的方式给出这两种操作的运行过程，最后再归纳出数学公式。
  注意：本文主要是结合Tensorflow来讲的，不同的平台会有所差异。

二、术语解释

  CNN网络的主要参数有下面这么几个：

  • 卷积核Kernal（在Tensorflow中称为filter）；
  • 填充Padding；
  • 滑动步长Strides；
  • 池化核Kernal（在Tensorflow中称为filter）；
  • 通道数Channels。

2.1 卷积核

  顾名思义，卷积核是在进行卷积操作的时候使用的，在Tensorflow中，被称为filter，通过一个四元列表传递。文档中对该参数的说明如下：

1
2
3
4
5
6
7
"""
filter: A `Tensor`. Must have the same type as `input`.
A 4-D tensor of shape
`[filter_height, filter_width, in_channels, out_channels]`
"""
# 定义一个大小为3*2，输入channel为3，输出channel为64的filter
conv_kernal = [3, 2, 3, 64]

  卷积核的示意图如下图中间部分（这里的卷积核大小为3*3）所示：

图2-1　　卷积核示意图

  由上图可知，卷积这一步的操作，实际上是在输入数据上取与卷积核大小相同的矩阵，然后与卷积核矩阵进行哈达马达乘积)，然后求这个乘积矩阵所有元素的和，作为卷积的结果。

  需要说明的是，这里的卷积跟我们信号与系统里面的卷积有所差异。

  上面提到的通道数（in_channels、out_channels）实际上就是我们的feature_map的数量。因为不同的卷积核卷积出来的feature_map是不一样的，因此有多少个out_channels，就有多少个不同的卷积核。关于这点，会在后边的通道参数里面解释。

  对于直接与输入层连接的卷积层来说，输入通道数in_channels，图片通常为3（因为包含R、G、B三色矩阵），文本则通常为1。

2.2 填充

  填充在卷积和池化这两个操作里面都可能会用到，填充的作用主要是尽可能充分的保留和使用输入特征（如果不使用填充，网络层数越深，所丢失的边缘数据就越多，到最后可能无特征可用），同时也应注意填充的尺寸不宜过大，避免引入过多无用的数据。
  关于填充作用的说明还可以参考知乎上的这篇文章。Tensorflow中的填充只有两种类型，说明如下：

1
2
3
4
5
6
"""
padding: A `string` from: `"SAME", "VALID"`.
         The type of padding algorithm to use.
"""
# VALID 对应的是不填充，即不做任何处理。
# SAME  这种填充方式在strides=1的情况下，使得输出能够保持和输入尺寸一致。

  Theano中的填充则有不填充、半填充、全填充三种，它的半填充对应Tensorflow的SAME。

  SAME类型以0进行填充的示意图如下：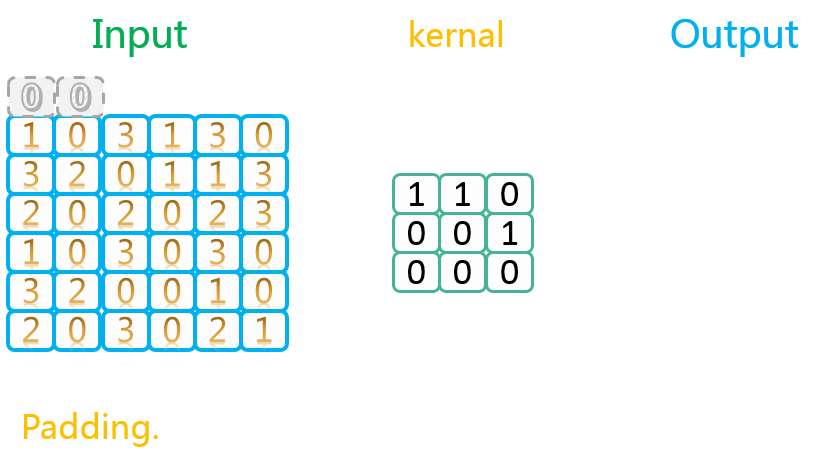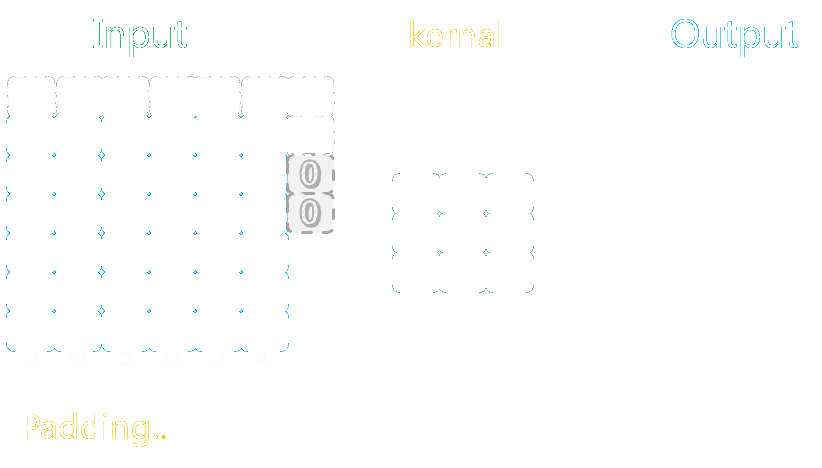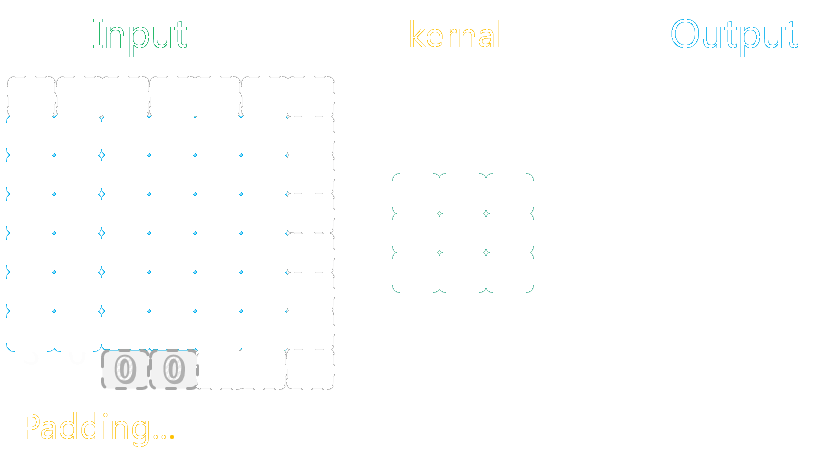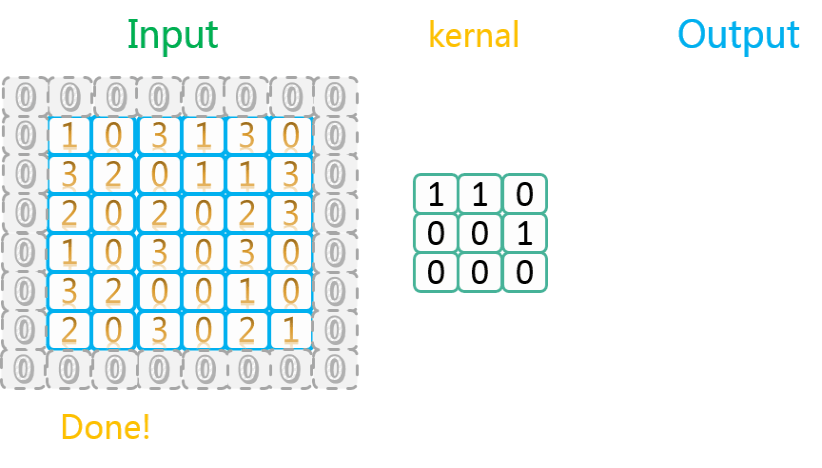

图2-2　　‘SAME’类型填零示意图

  可以看到，这个操作实际上是在原始数据外面包裹了一层填充数据。

2.3 滑动步长

  滑动步长决定了在卷积或者池化的过程中，每次操作后移动的步数。在Tensorflow中，该参数也是一个四元列表，关于该参数的解释如下：

1
2
3
4
5
6
7
8
"""
strides: A list of `ints`.
  1-D tensor of length 4.  The stride of the sliding window for each
  dimension of `input`. The dimension order is determined by the value of `data_format`, see below for details.
  strides = [batch, height, width, channels]
"""
# 定义一个不跳过任何样本、不跳过任何颜色通道，垂直方向步长为2，水平方向步长为2的strides
strides = [1, 2, 2, 1]

  它的第2、3个参数分别对应在数据垂直和水平方向上的滑动步长。第1个参数表示在样本上的跳跃幅度，一般都是置为1（表示不会跳过任何样本）。第4个参数表示在通道上的跳跃幅度，通常也是置为1。更详细的可参见Stackoverflow上的讨论以及该博客。

  卷积过程中的滑动过程示意如下：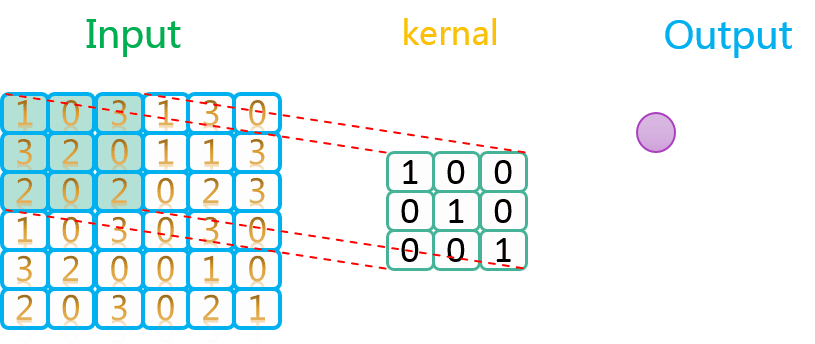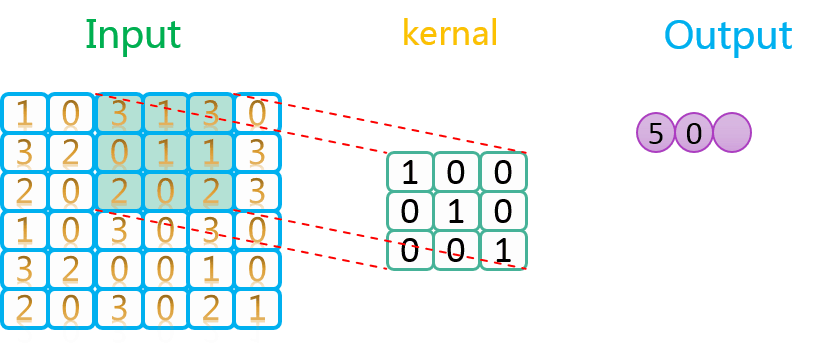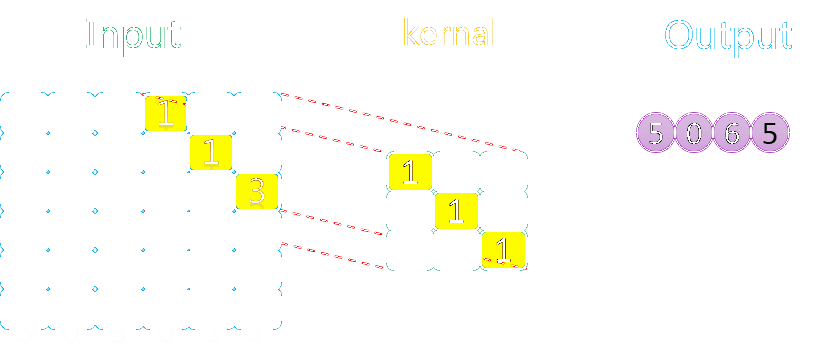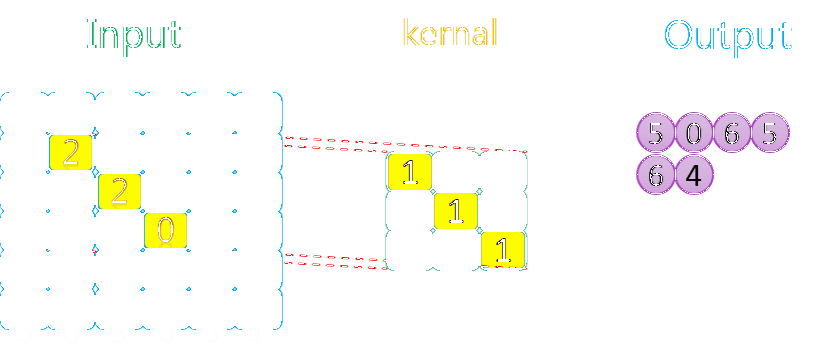

图2-3　　步长为1时的滑动示意图

  由上图可知，卷积核在输入数据上的操作顺序是先沿着水平方向，再沿着垂直方向。因为水平方向上步长为1，所以卷积核在水平方向上每操作一次，就往右移动一格，再进行下一次操作。当水平方向上操作完了以后，就回到最左边，在垂直方向向下移动一格，然后进行操作，如此往复循环，直到所有数据均处理完。

  此外需要说明的是，由于卷积核中值为0的部分对最终的结果没有任何贡献，因此在动图中卷积的时候没有高亮（黄色）显示，并不代表它们没有参与卷积。另外输入和卷积核的元素可以是任意值（上图只是为方便举的简单例子）。

  如果你把卷积核看做单反的取景框，把输入数据当作我们的风景，卷积核在输入上的移动过程就类似于我们拍全景照的过程，从左往右，从上往下。

  我们再来看看水平、垂直方向上滑动步长均为2并且使用了SAME方式填充的情况，如下图所示：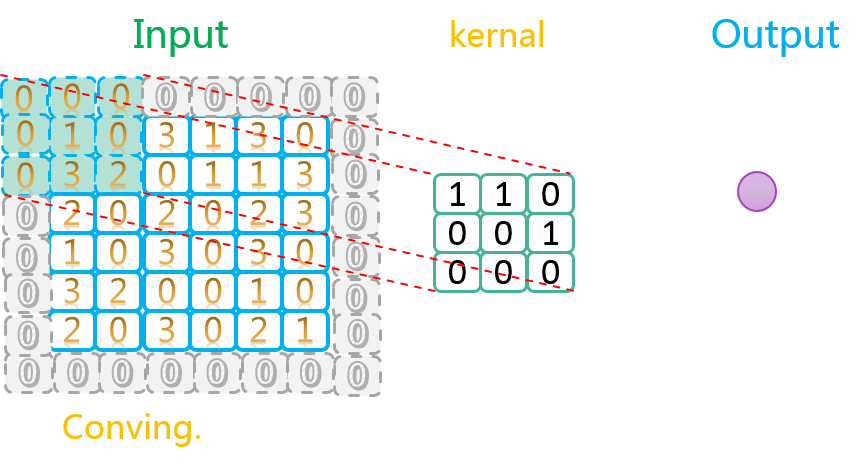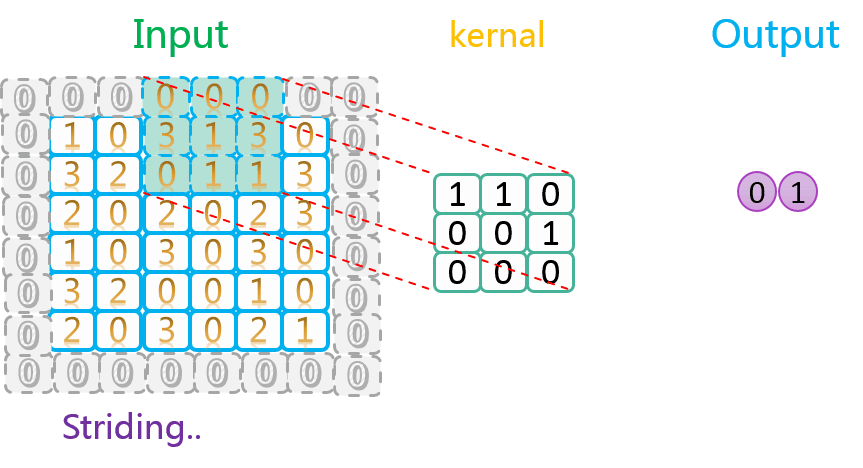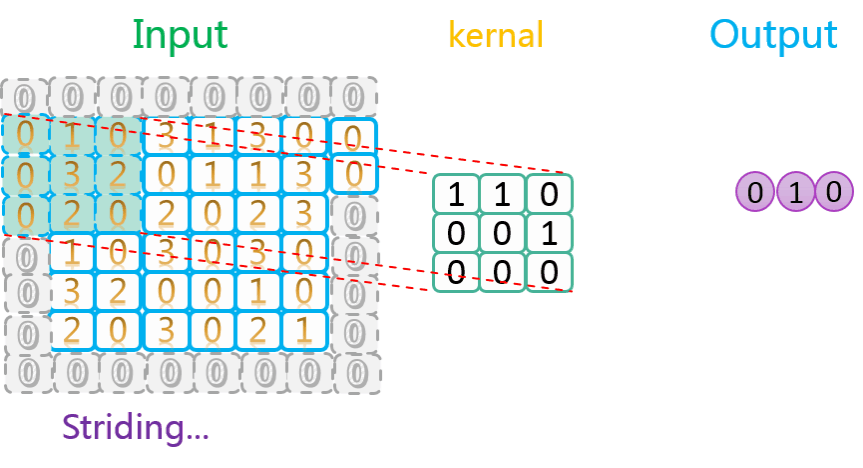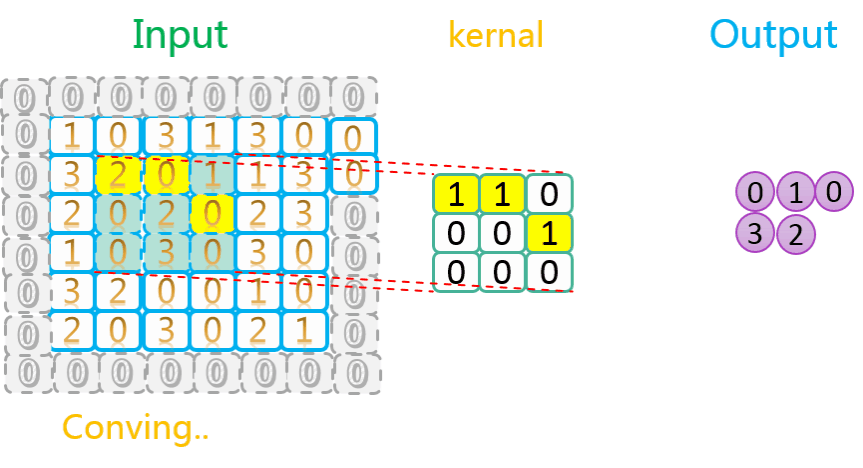

图2-4　　步长为2时的滑动示意图

  由上图可知，其操作流程与步长为1时并没有区别，只不过每次沿水平/垂直方向挪动的步长为2。另外不太一样的地方是，对于有填充的数据，卷积核的取景（取值）范围不会超出填充数据（第一行最后一次移动）。

2.4 池化核

  池化核则是在进行池化操作时候的Kernal，池化的作用类似于PCA，可以有效的对数据降维同时保留关键特征。常用的池化核有如下几种类型：

  • 最大池化核，取池化数据（取景框取出来的所有数据）的最大值；
  • 平均池化核，取池化数据的平均值；
  • 最小池化核，取池化数据的最小值；
  • L2池化核，取池化数据的L2范数；

  下图分别展示了步长分别为1、2时的最大池化过程：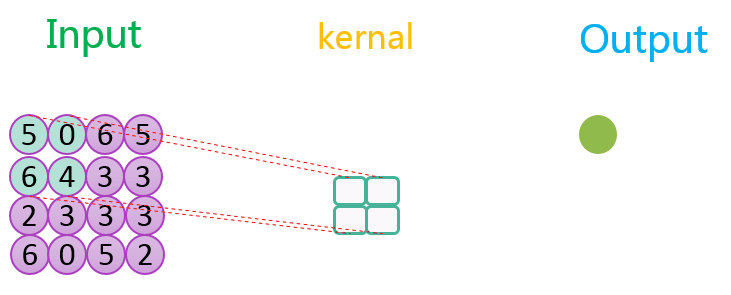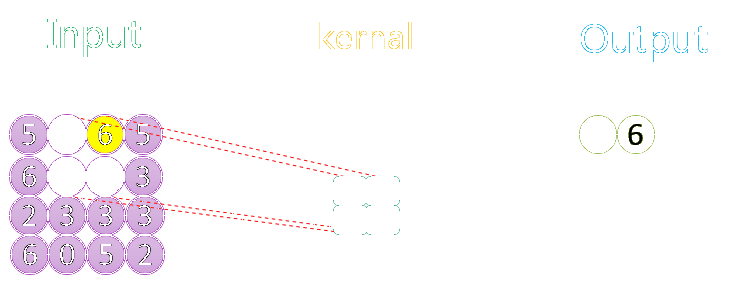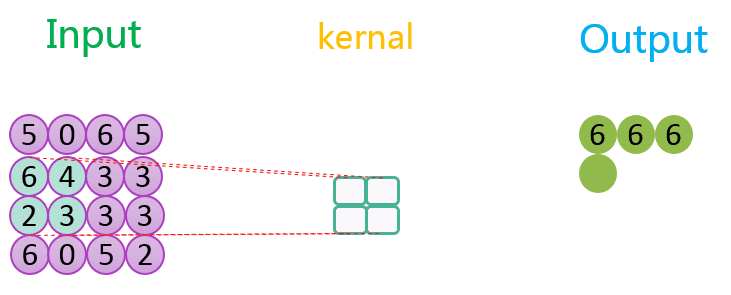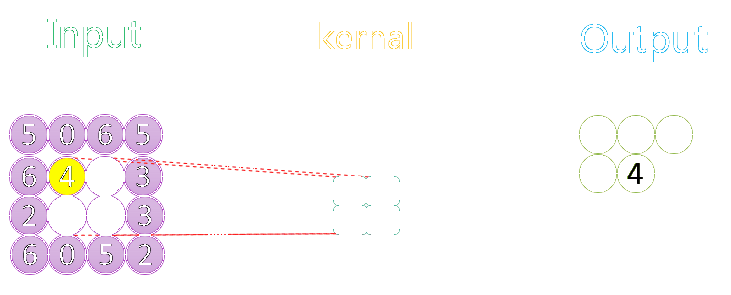

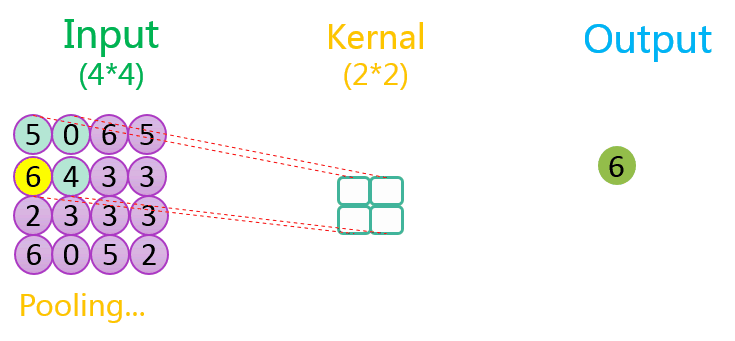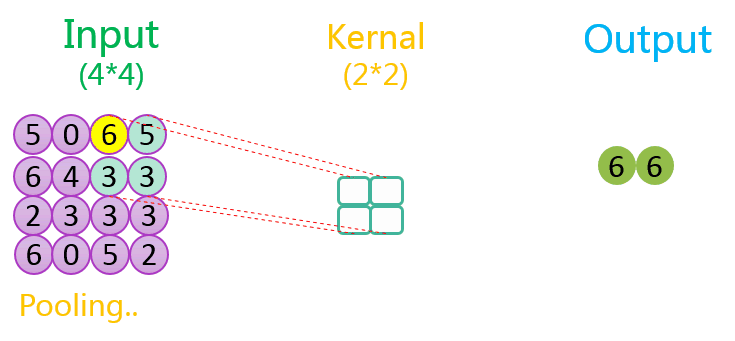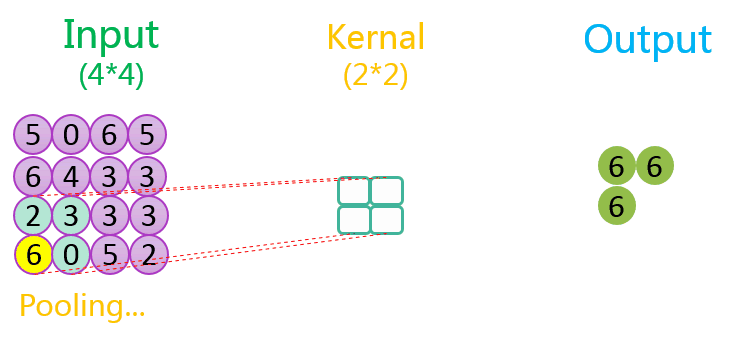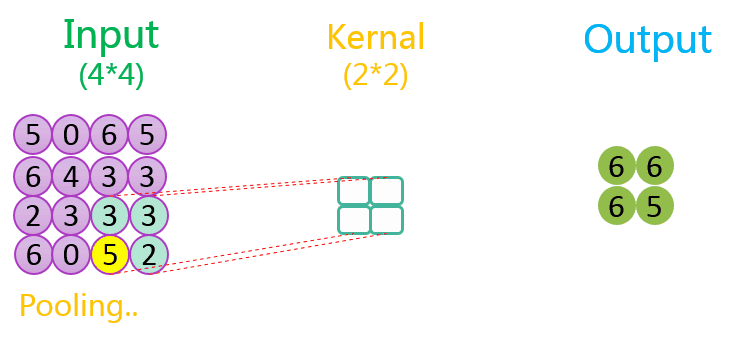
图2-5　　步长为1时的最大池化示意图

图2-6　　步长为2时的最大池化示意图

  关于池化的作用可参考该CSDN博客。

2.5 通道数

  从上面的介绍我们可以看出，对于同一个输入矩阵，改变卷积核的元素值，将会产生不同的输出。因此，卷积核的数量决定了卷积操作之后生成的feature map（卷积核在输入上卷积后的输出矩阵我们称为feature map）数量。

  对于CNN来说，其隐藏层部分，上一层的卷积核（即为该层的输出通道数out_channels）数量决定了下一层的输入通道数(in_channels)。输入层部分，输入的类型决定了第一个隐藏层的输入通道数。对于图片数据来说，会拆分成3个输入矩阵，分别对应RGB三原色，如下图所示：

图2-7　　彩色图片三通道示意图（图片摘自网络）

图2-8　　彩色图片三通道输入矩阵示意图（图片摘自网络博客 ）

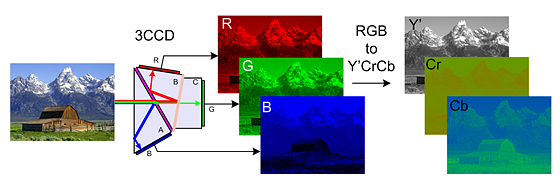
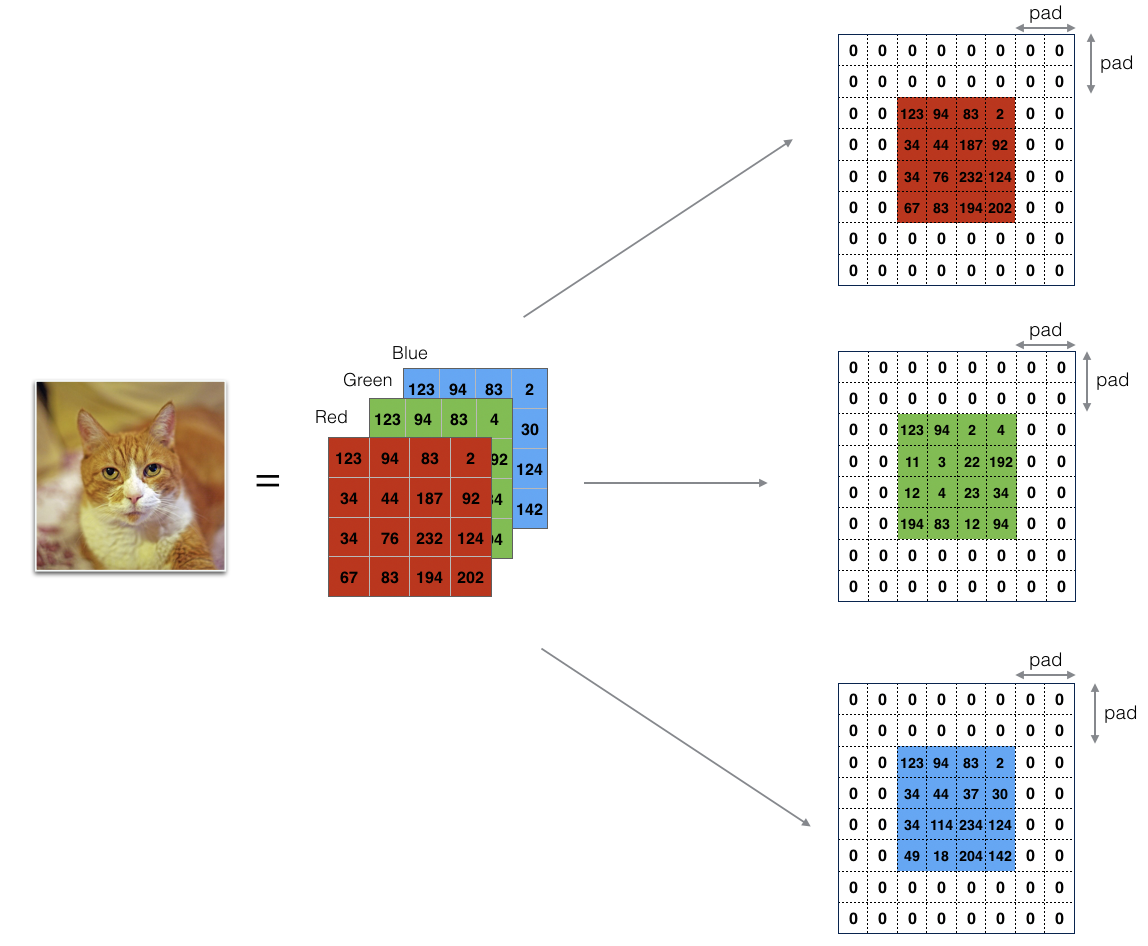
  当然图片如果是以CMYK格式存储的，那么输入通道数就会变成4个。而对于文本类的输入，其通道数则只有1个。当然，也可以通过reshape操作后把文本输入变成3通道的数据（将文本数据模拟成图像，360曾经把网络流量转换成黑白图片，并用来训练DNN模型，从而判别是否包含恶意数据，这个想法真的是非常有创意。详见这里）。

  总之，数据是死的，人脑是活的，怎么玩，就靠你自己去发挥想象力了。下图是步长为2，卷积核数量为2上的卷积过程示意图：

图2-9　　步长为2、卷积核数量为2无填充情况的卷积示意图

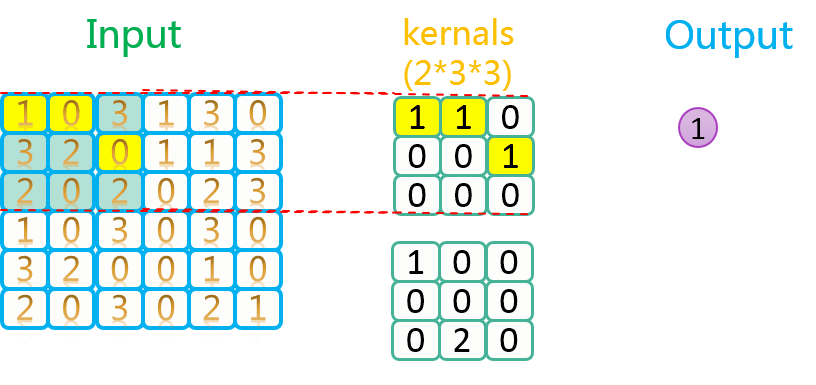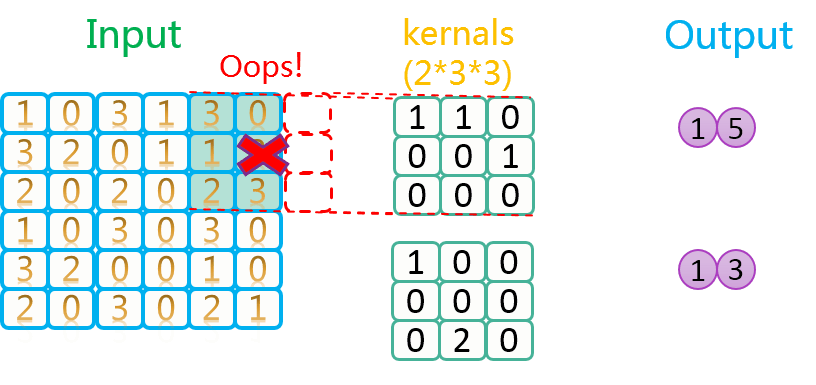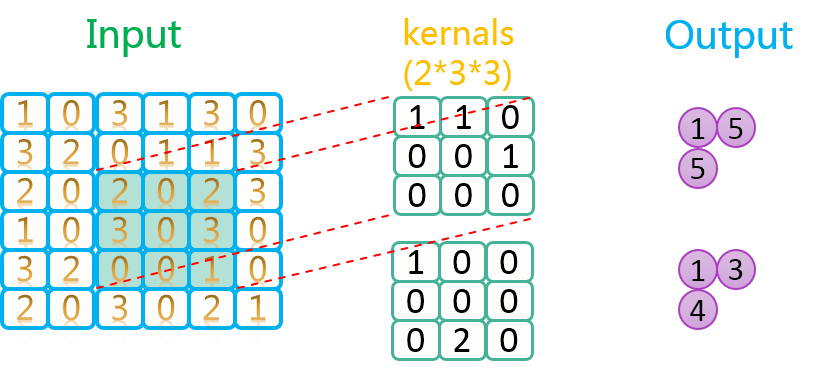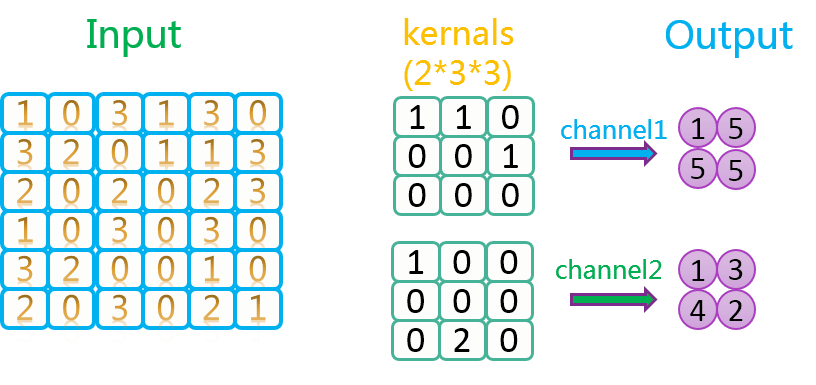
三、参数计算

  主要有两个部分的参数需要计算，一个是卷积后的尺寸，另一个是池化后的尺寸。先看一些具体的比较简单的例子，方便去数。最后再给出通用的计算公式。

3.1 卷积后的尺寸

3.1.1 无填充、步长为1

  整个过程如下所示：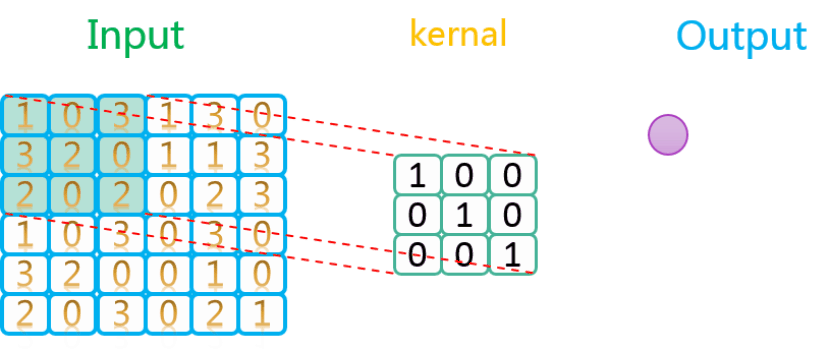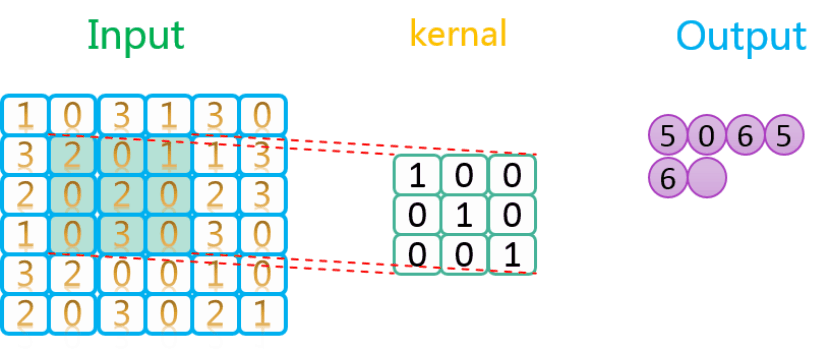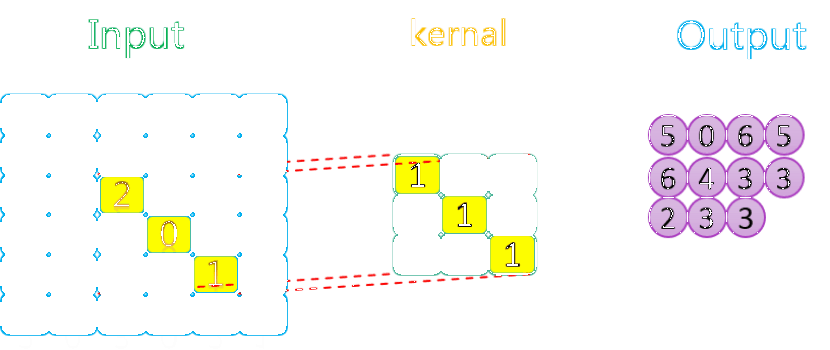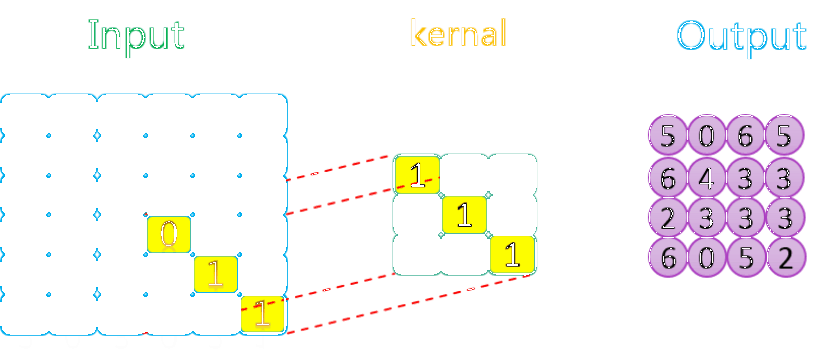

图3-1　　无填充步长为1卷积示意图

  如上图所示，相关数据如下表所示：

输入通道数
（个）		 输入尺寸
（高*宽）		 卷积核数量
（个）		 卷积核尺寸
（高*宽）		 步长
（步）		 输出通道数
（个）		 输出尺寸
（高*宽）		 填充
1 6 * 6 1 3 * 3 1 1 4 * 4 VALID

3.1.2 无填充、步长为2

  整个过程如下所示：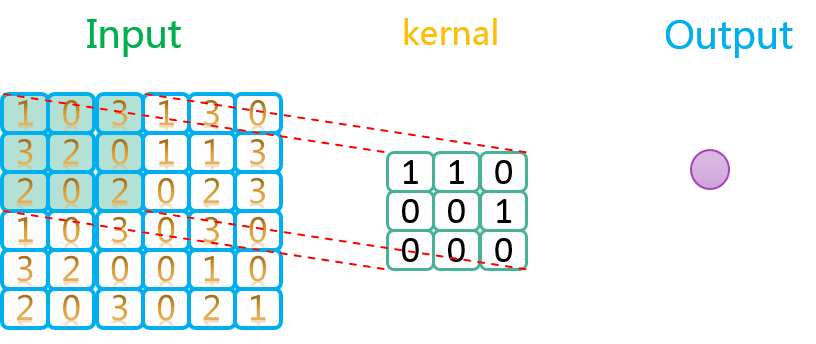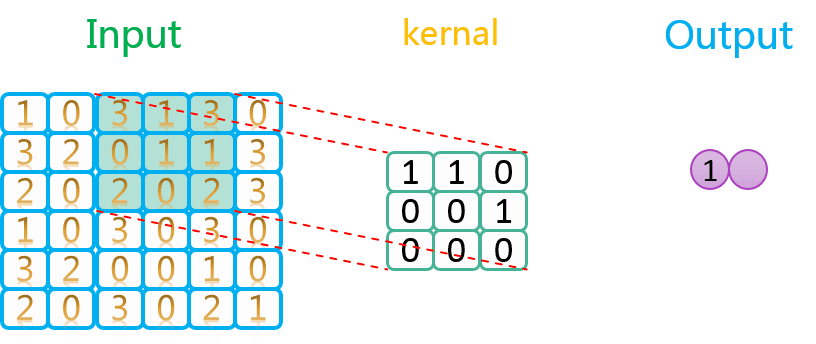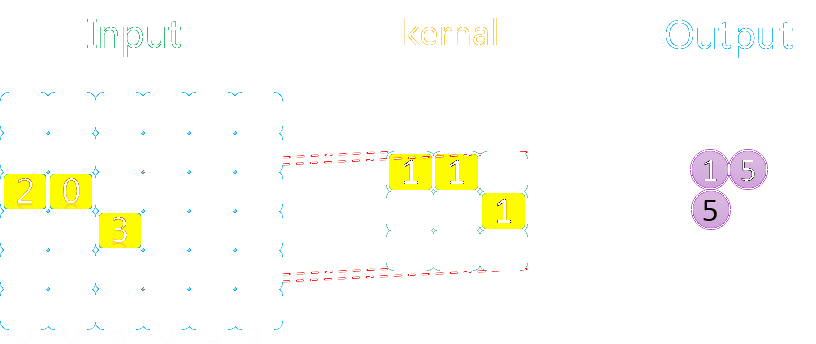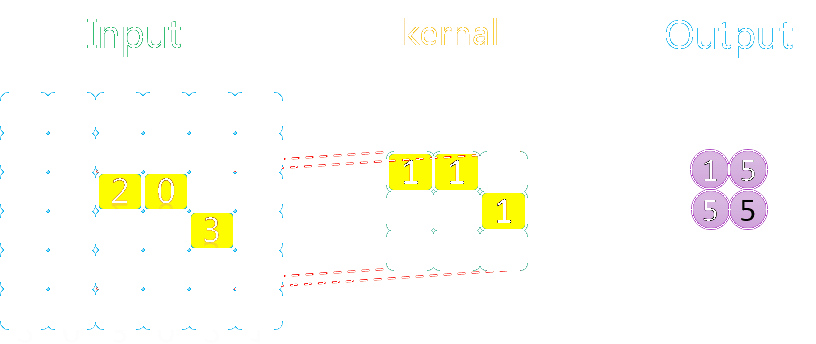

图3-2　　无填充步长为2卷积示意图

  如上图所示，相关数据如下表所示：

输入通道数
（个）		 输入尺寸
（高*宽）		 卷积核数量
（个）		 卷积核尺寸
（高*宽）		 步长
（步）		 输出通道数
（个）		 输出尺寸
（高*宽）		 填充
1 6 * 6 1 3 * 3 2 1 2 * 2 VALID

  由上述两图、表可知，除卷积核大小外其它所有条件都不变的情况下，第二种情况相较于第一种情况，其输出的尺寸缩小了$\frac{2}{4} * \frac{2}{4} = \frac{1}{4}$，高、宽各自方向上则缩小了$\frac{2}{4} = \frac{1}{2}$。

3.1.3 有填充、步长为2

  整个过程如下所示：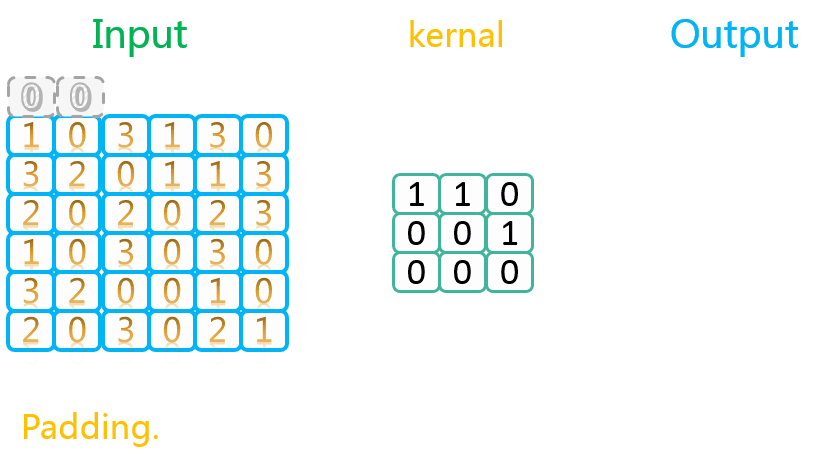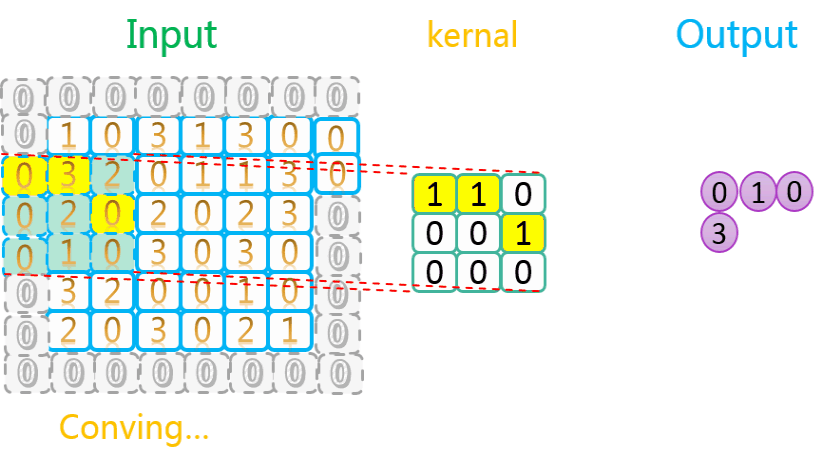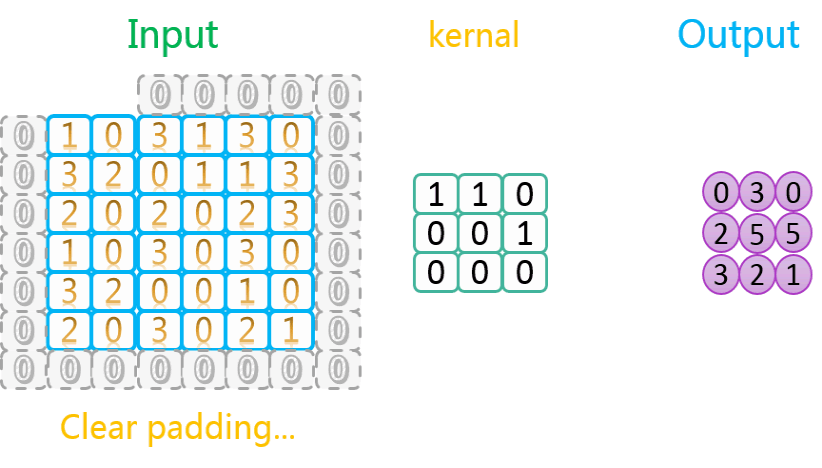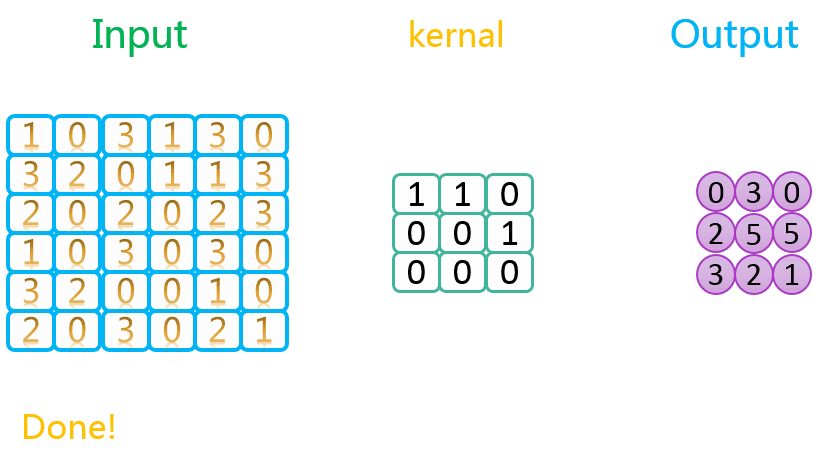

图3-3　　有填充步长为2卷积示意图

  如上图所示，相关数据如下表所示：

输入通道数
（个）		 输入尺寸
（高*宽）		 卷积核数量
（个）		 卷积核尺寸
（高*宽）		 步长
（步）		 输出通道数
（个）		 输出尺寸
（高*宽）		 填充
1 6 * 6 1 3 * 3 2 1 3 * 3 SAME(8*8)

3.2 池化后的尺寸

3.2.1 无填充、步长为1

  整个过程如下所示：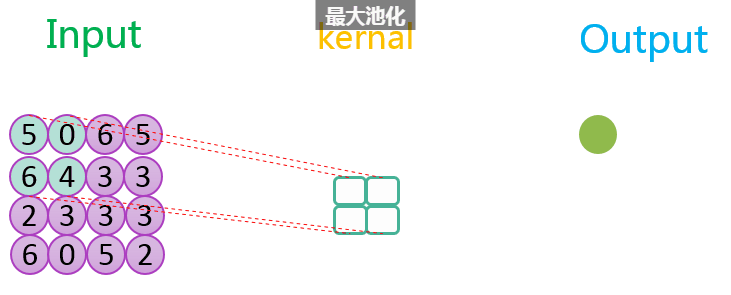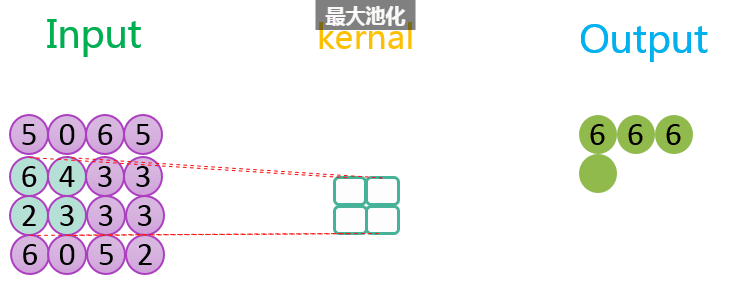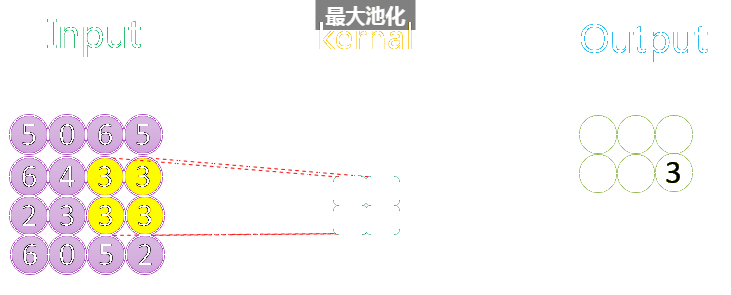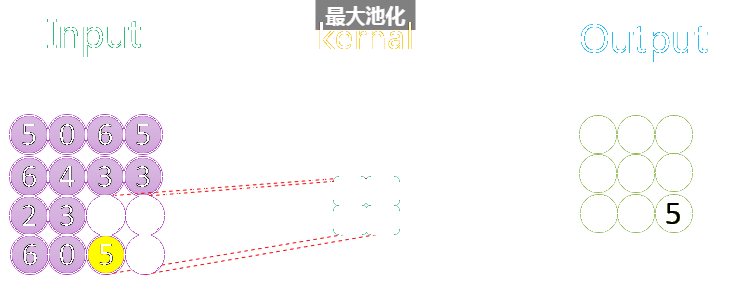

图3-4　　无填充步长为1池化示意图

  如上图所示，相关数据如下表所示：

输入通道数
（个）		 输入尺寸
（高*宽）		 池化核数量
（个）		 池化核尺寸
（高*宽）		 步长
（步）		 输出通道数
（个）		 输出尺寸
（高*宽）		 填充
1 4 * 4 1 2 * 2 1 1 3 * 3 VALID

3.2.2 无填充、步长为2

  整个过程如下所示：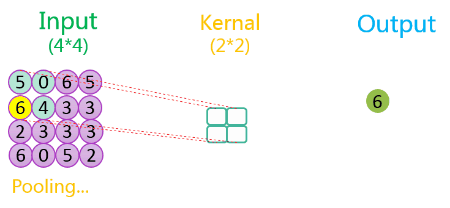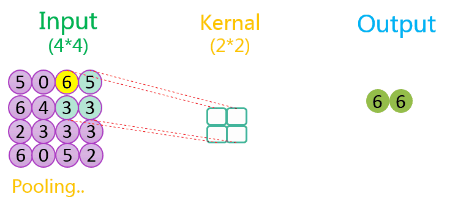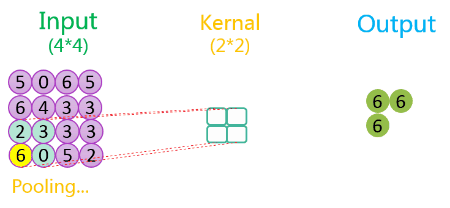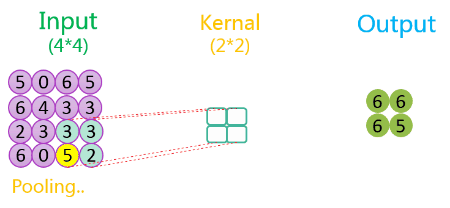

图3-5　　无填充步长为2池化示意图

  如上图所示，相关数据如下表所示：

输入通道数
（个）		 输入尺寸
（高*宽）		 池化核数量
（个）		 池化核尺寸
（高*宽）		 步长
（步）		 输出通道数
（个）		 输出尺寸
（高*宽）		 填充
1 4 * 4 1 2 * 2 2 1 2 * 2 VALID

3.2.3 有填充、步长为2

  整个过程如下所示：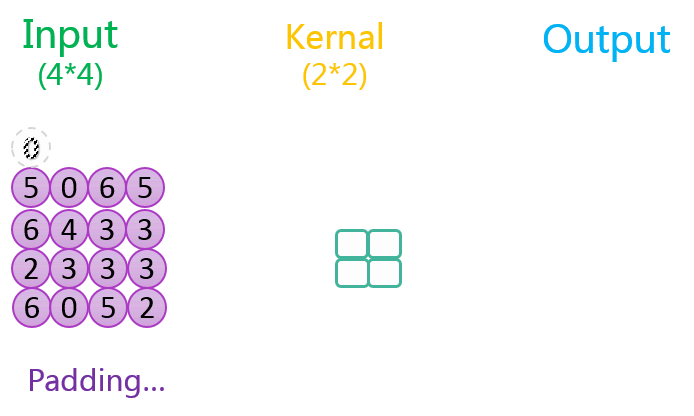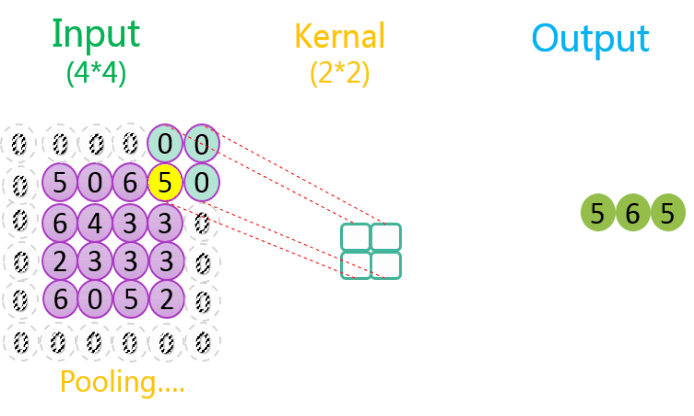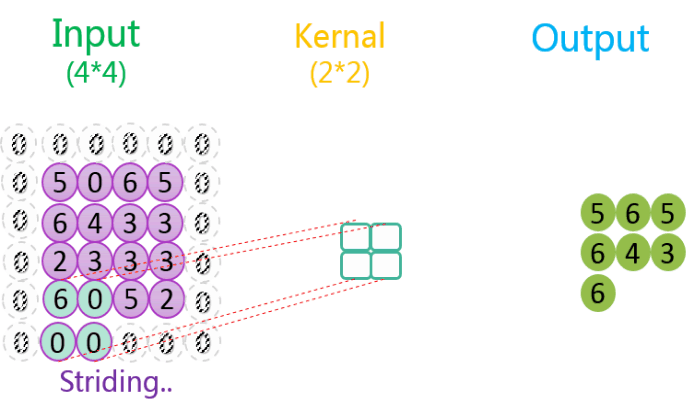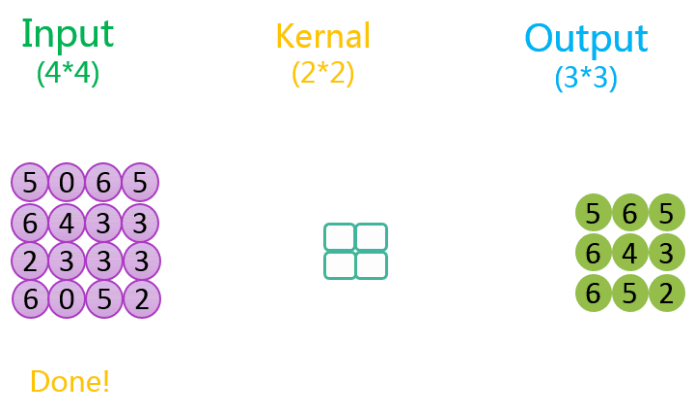

图3-6　　有填充步长为2池化示意图

  如上图所示，相关数据如下表所示：

输入通道数
（个）		 输入尺寸
（高*宽）		 池化核数量
（个）		 池化核尺寸
（高*宽）		 步长
（步）		 输出通道数
（个）		 输出尺寸
（高*宽）		 填充
1 4 * 4 1 2 * 2 2 1 3 * 3 SAME(8*8)

3.3 计算公式

  卷积后的参数无非就三个，通道数、高、宽。其中通道数不用计算，就等于卷积核数量。为方便叙述，记：

  • $H_{in}$，输入矩阵行数（像素高度）；
  • $H_{out}$，输出矩阵行数（像素高度）；
  • $W_{in}$，输入矩阵列数（像素宽度）；
  • $W_{out}$，输出矩阵列数（像素宽度）；
  • $H_{ker}$，卷积/池化核矩阵行数（高度）；
  • $W_{ker}$，卷积/池化核矩阵列数（宽度）；
  • $CH_{in}$，输入通道数；
  • $CH_{out}$，输出通道数；
  • $S$，步长；
  • $K$,卷积/池化核数量；
  • $P$，填充数量（VALID时为0，SAME时为1）；
  • $\left \lceil \quad \right \rceil$，向上取整（等价于Python中的math.ceil()函数）；

3.3.1 卷积部分推导

  给定相关参数后，设卷积核在水平、垂直方向分别可以有效移动（对有填充情况，超出填充部分则该次移动无效。无填充情况，超出输入数据则移动无效。）$m、n$次，则有：

3.3.1.1 水平方向

  移动情况如下所示：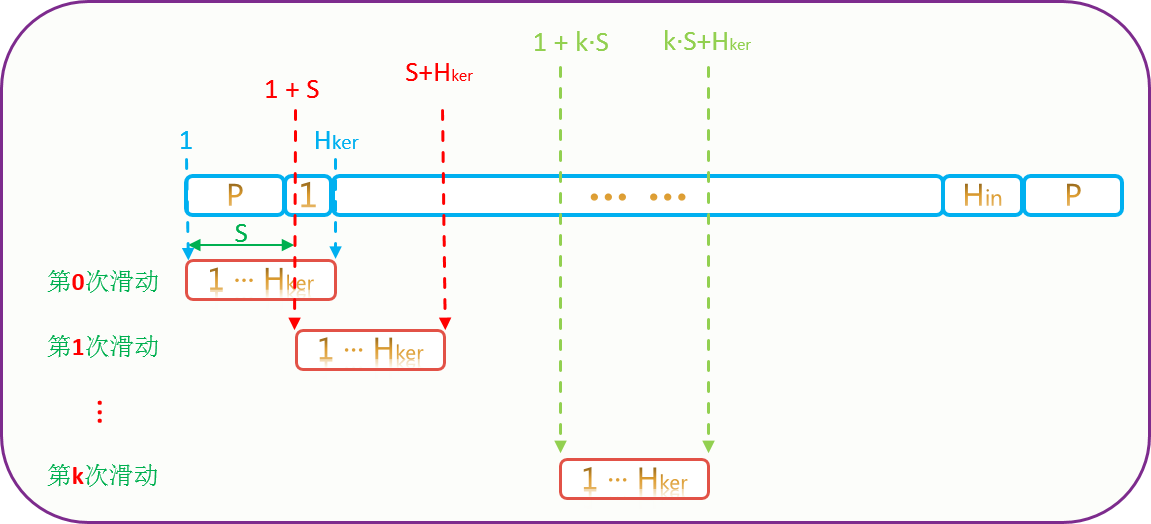

图3-4　　水平方向移动示意图

  由图有：

$$
m \cdot S + H_{ker} \leq H_{in} + 2 \cdot P \\\\
\tag{3 - 1}
$$

  可求得：

$$
m \leq \frac{(H_{in} + 2 \cdot P - H_{ker})}{S} \\\\
\tag{3 - 2}
$$

  而$H_{out}$就是我们最大的滑动次数，即：

$$
H_{out} = m_{max} + 1= \left \lfloor \frac{(H_{in} + 2 \cdot P - H_{ker})}{S} \right \rfloor + 1= \frac{(H_{in} + 2 \cdot P - H_{ker})}{S} + 1\\\\
\tag{3 - 3}
$$

  注意：上式中$m_{max}$还要加1，因为第0次滑动的时候，也是做了卷积操作的。对应的文字版公式为：

$$
输出宽度 = \frac{(输入宽度 + 2 \cdot 填充宽度 - 卷积核宽度)}{步长} + 1\\\\
\tag{3 - 4}
$$

3.3.1.2 垂直方向

  垂直方向的推导与水平方向一致，只不过换了个方向而已，在此不赘述，直接给出其计算公式如下：

$$
W_{out} = n_{max} + 1= \left \lfloor \frac{(W_{in} + 2 \cdot P - W_{ker})}{S} \right \rfloor + 1= \frac{(W_{in} + 2 \cdot P - W_{ker})}{S} + 1\\\\
\tag{3 - 5}
$$

  对应的文字版公式为：

$$
输出高度 = \frac{(输入高度 + 2 \cdot 填充高度 - 卷积核高度)}{步长} + 1\\\\
\tag{3 - 6}
$$

3.3.1.3 结论

  综上，再加入输出通道数，有卷积操作后输出的尺寸的计算公式如下：

$$
\begin{cases}
\begin{split}
H_{out} &= \left \lfloor \frac{(H_{in} + 2 \cdot P - H_{ker})}{S} \right \rfloor + 1= \frac{(H_{in} + 2 \cdot P - H_{ker})}{S} + 1\\\\
W_{out} &= \left \lfloor \frac{(W_{in} + 2 \cdot P - W_{ker})}{S} \right \rfloor + 1= \frac{(W_{in} + 2 \cdot P - W_{ker})}{S} + 1 \\\\
CH_{out} &= K
\end{split}
\end{cases}
\tag{3 - 7}
$$

  对应的文字版公式为：

$$
\begin{cases}
\begin{split}
输出宽度 &= \frac{(输入宽度 + 2 \cdot 填充宽度 - 卷积核宽度)}{步长} + 1\\\\
输出高度 &= \frac{(输入高度 + 2 \cdot 填充高度 - 卷积核高度)}{步长} + 1 \\\\
输出通道数 &= 卷积核数量
\end{split}
\end{cases}
\tag{3 - 8}
$$

  如果有疑问，可以把前面的例子拿来验证。Tensorflow中关于这部分的说明参考官方文档。

3.3.2 池化部分推导

  池化部分因为工作原理和卷积部分基本上是一样的，所以其公式推导也并没有什么不同，有一点需要指出的是，池化部分仍然可以有填充。池化部分的推导这里就不再赘述。

3.3.3 小结

3.3.3.1 公式整合

  综上，整理出卷积/池化参数的通用计算公式如下：

$$
\begin{cases}
\begin{split}
H_{out} &= \left \lfloor \frac{(H_{in} + 2 \cdot P - H_{ker})}{S} \right \rfloor + 1= \frac{(H_{in} + 2 \cdot P - H_{ker})}{S} + 1\\\\
W_{out} &= \left \lfloor \frac{(W_{in} + 2 \cdot P - W_{ker})}{S} \right \rfloor + 1= \frac{(W_{in} + 2 \cdot P - W_{ker})}{S} + 1 \\\\
CH_{out} &= K
\end{split}
\end{cases}
\tag{3 - 9}
$$

  对应的文字版公式为：

$$
\begin{cases}
\begin{split}
输出宽度 &= \frac{(输入宽度 + 2 \cdot 填充宽度 - 卷积/池化核宽度)}{步长} + 1\\\\
输出高度 &= \frac{(输入高度 + 2 \cdot 填充高度 - 卷积/池化核高度)}{步长} + 1 \\\\
输出通道数 &= 卷积/池化核数量
\end{split}
\end{cases}
\tag{3 - 10}
$$

  使用式（3-9）最右边的表达式计算时一定要注意，这种表达不是特别严谨，这样写是为了兼容网络上的一些博客的写法，分式结果要记得向下取整。

3.3.3.2 参考资料

  大部分参考的文献资料都在相应位置给出了，剩下还有些参考的资料罗列如下：

3.4 示例

  举几个例子来验证下。

3.4.1 示例1

  该例子是牛客网上题库中的一个题，试题如下：

  输入图片大小为200×200，依次经过一层卷积（kernel size 5×5，padding 1，stride 2），pooling（kernel size 3×3，padding 0，stride 1），又一层卷积（kernel size 3×3，padding 1，stride 1）之后，输出特征图大小为：
A. 95
B. 96
C. 97
D. 98
E. 99
F. 100
答案： C

  可以看出，该网络隐藏层共有3层（2层卷积，1层池化），再加上输入、输出层，该网络是一个5层的NN。

  对第一层卷积层，我们有$H_{in} = W_{in} = 200, \ H_{ker} = W_{ker} =5, \ S = 2, \ P = 1, \ K = ?$，则根据公式（3-9）有：

$$
\begin{cases}
\begin{split}
H_{out} &= \left \lfloor \frac{(H_{in} + 2 \cdot P - H_{ker})}{S} \right \rfloor + 1 = \left \lfloor \frac{(200 + 2 \times 1 - 5)}{2} \right \rfloor + 1 = 99\\\\
W_{out} &= \left \lfloor \frac{(H_{in} + 2 \cdot P - H_{ker})}{S} \right \rfloor + 1 = \left \lfloor \frac{(200 + 2 \times 1 - 5)}{2} \right \rfloor + 1 = 99
\end{split}
\end{cases}
\tag{3 - 11}
$$

  对第二层池化层，同理我们有$H_{in} = W_{in} = 99, \ H_{ker} = W_{ker} =3, \ S = 1, \ P = 0, \ K = ?$，则有：

$$
\begin{cases}
\begin{split}
H_{out} &= \left \lfloor \frac{(99 + 2 \times 0 - 3)}{1} \right \rfloor + 1 = 97\\\\
W_{out} &= \left \lfloor \frac{(99 + 2 \times 0 - 3)}{1} \right \rfloor + 1 = 97
\end{split}
\end{cases}
\tag{3 - 12}
$$

  对第三层池化层，同理我们有$H_{in} = W_{in} = 97, \ H_{ker} = W_{ker} =3, \ S = 1, \ P = 1, \ K = ?$，则有：

$$
\begin{cases}
\begin{split}
H_{out} &= \left \lfloor \frac{(97 + 2 \times 1 - 3)}{1} \right \rfloor + 1 = 97\\\\
W_{out} &= \left \lfloor \frac{(97 + 2 \times 1 - 3)}{1} \right \rfloor + 1 = 97
\end{split}
\end{cases}
\tag{3 - 13}
$$

3.4.2 示例2

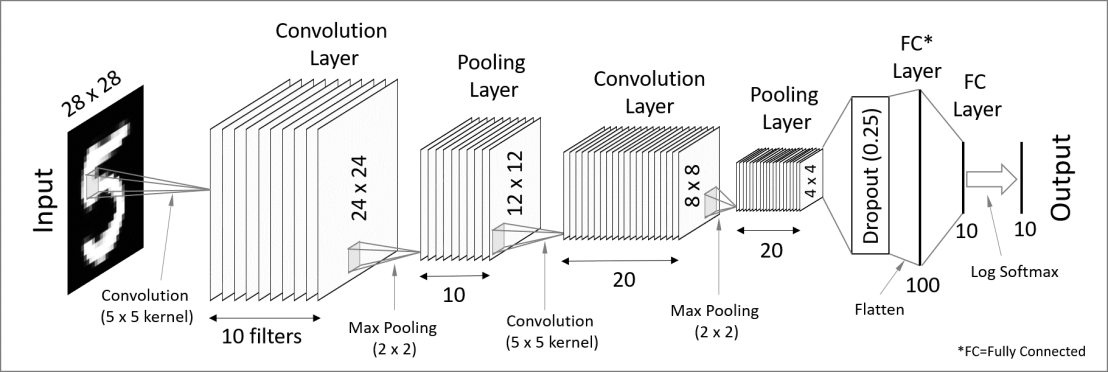
  该例子是经典的LeNet-5，网络结构如下图所示：

图3-5　　LeNet-5网络结构图（图片摘自Paper）

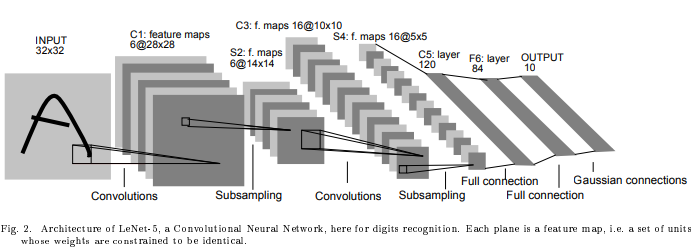
  其网络参数参考下图（卷积核大小均为5*5，步长1。池化核大小均为2*2，步长为2，通道数不定。）：

层数 层类型 对应名称 相关参数
1 输入层 INPUT 输入尺寸 32 * 32 * 1
2 第1个卷积层 C1 卷积核尺寸 5 * 5 * 6, 步长 1, 填充 VALID
3 第1个池化层 S2 池化核尺寸 2 * 2 * 6, 步长 2, 填充 VALID
4 第2个卷积层 C3 卷积核尺寸 5 * 5 * 16, 步长 1, 填充 VALID
5 第2个池化层 S4 池化核尺寸 2 * 2 * 16, 步长 2, 填充 VALID
6 第3个卷积层 C5 卷积核尺寸 5 * 5 * 120, 步长 1, 填充 VALID
7 第1个全连接层 F6 压扁为84个神经元
8 输出层 OUTPUT 10种分类

  第1个卷积层C1，有：

$$
W_{out} = H_{out} = \left \lfloor \frac{(32 + 2 \times 0 - 5)}{1} \right \rfloor + 1 = 28
\tag{3 - 14}
$$

  第1个池化层S2，有：

$$
W_{out} = H_{out} = \left \lfloor \frac{(28 + 2 \times 0 - 2)}{2} \right \rfloor + 1 = 14
\tag{3 - 15}
$$

  第2个卷积层C3，有：

$$
W_{out} = H_{out} = \left \lfloor \frac{(14 + 2 \times 0 - 5)}{1} \right \rfloor + 1 = 10
\tag{3 - 16}
$$

  第2个池化层S4，有：

$$
W_{out} = H_{out} = \left \lfloor \frac{(10 + 2 \times 0 - 2)}{2} \right \rfloor + 1 = 5
\tag{3 - 17}
$$

  第2个池化层S4，有：

$$
W_{out} = H_{out} = \left \lfloor \frac{(10 + 2 \times 0 - 2)}{2} \right \rfloor + 1 = 5
\tag{3 - 18}
$$

  第3个卷积层C5，有：

$$
W_{out} = H_{out} = \left \lfloor \frac{(5 + 2 \times 0 - 5)}{1} \right \rfloor + 1 = 1
\tag{3 - 19}
$$

  第1个全连接层F6（全连接层没有卷积/池化操作），有：

$$
\begin{cases}
\begin{split}
H_{out} &= 1 \\\\
W_{out} &= 84
\end{split}
\end{cases}
\tag{3 - 20}
$$

  所有结果计算出来都与原始Paper吻合，证明我们的公式是准确无误的。