特征值和特征向量内幕详解 | 断鸿声里，立尽斜阳

All in matrix.

起源

1. 概述

这篇博客的诞生源自在做之前的项目时想基于PCA构建一些新的Idea，于是就需要深入的去理解PCA。PCA可以用来降维这点相信大家都是知道的，也有很多开源的库(如scikit-learn)都直接实现了，几行调用就能搞定，极大的方便了我们。

正是这种便利性让其背后所蕴含的复杂的数学原理被深深的掩藏了起来。这就导致很多人以为自己已经掌握了PCA算法的精髓，洞悉了其背后的真相。毫无疑问，在这篇博客成稿之前，我也是其中的一个。

意识到自己对特征值和特征向量的理解原来一直停留在一个很肤浅的层面是随着项目的深入不断确认的。我只是记住了如何用这些数字去套对应的公式，却没能从根本上去思考和理解为什么要这样做，为什么能这样做。对于理工科学生来说，这是一个非常严重的问题。

而据我了解，有相当大比例的理工科学生都存在这样的问题，那么这个锅就完全该学生来背吗？

师者，所以传道授业解惑也！

不尽然。国内高校教育方式的古板与僵化要负很大责任。绝大部分老师做到了传道，极少部分能做到授业，而只有屈指可数的能真正做到解惑。印象中能够把教材上的大部分公式用自己的语言（而不是照本宣科）完整的推导证明（板书）一遍的老师，已经算是可遇而不可求了。

考虑到读者的专业背景迥异，对相关概念的理解也千差万别。因此本文会先从一些较为基础的概念起步，力求从更加形象（几何）的角度去解读特征值(eigenvalue)和特征向量(eigenvector)这两个概念，从而帮助读者平滑的过渡到相关的知识体系中。

此外，在本博客成文之前，笔者也在网上进行过大量的搜索过，然而并没有找到一篇真正从源头解释清楚这两个专业术语的文章（包括群英荟萃的知乎）。因此本文的另一个重要出发点便是：从源头去阐释。

鉴于有些知识点远非三言两语能解释清楚的，因此本博文在篇幅上会不可避免的有些冗长，但如果你能耐心的看完，相信一定会有所收获。

概念

2. 基础概念

2.1 向量

说到向量，我们最早接触这个东西是在高中的时候。那个时候教材对于向量的定义比较简单：一条具备三要素即起点、终点、方向的线段，比如下面这样：

图2-1　　二维平面中的向量

又或者这样：

图2-2　　三维空间中的向量

是的，就是这么简单。现在看来高中那会儿所有的事情都是简简单单的。然而上了大学很多事就不再那么简单粗暴了。以向量来说，理工科对其概念做了延伸和扩展。下面我们将分别简述物理、计算机、数学三个方向的向量的定义。

2.1.1 物理学的向量

物理学中的向量，不太关注它的起点，而更侧重于其方向、大小（箭头长度）。只要这两个参数相同，不管如何移动，在物理学中始终认为它们是同一个向量。而物理学里面的向量通常是有着非常明确而清晰的几何意义的，比如带电粒子受到的洛伦兹力：

图2-3　　带电粒子的洛伦兹力

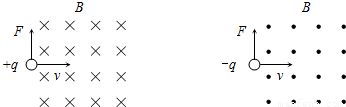
2.1.2 计算机的向量

计算机中的向量，通常是指一组有序的数字列表（C/C++以及Java中的数组、Python中的列表等），比如：

# python tuple
vector1 = (3, 5, 2, 9, 7)
# python list
vector2 = [2, 4, 0.6, 3, 1.3]

对于现在较为火热的机器/深度学习领域，一个向量通常代表一个具体的样本，而向量的每个元素，则表示相应的特征属性的取值。这个时候的向量通常并没有具体的几何含义与之对应。

2.1.3 数学的向量

数学中的向量则是兼具了物理学的概念清晰和计算机的通用性优点，同时对向量的定义和运算进行了严格的规定，并提供了严谨的理论证明，比如：

图2-4　　数学中的向量

2.1.4 表示形式

如上所述，向量在不同的领域其表示形式也不尽相同甚至大相径庭。在几何学中，向量通常用一对圆括号包裹，并且是横着书写，如：

$$
\vec w = (3, 2, 5)
\tag {几何表示}
$$

而向量在线性代数中的矩阵表达式则为：

$$
\vec w =
\begin{bmatrix}
3\\\\
2\\\\
5
\end{bmatrix} 或 \
\begin{bmatrix}
3\ \ 2\ \ 5
\end{bmatrix}^T
\tag {线代表示}
$$

以上两种形式无所谓好坏，本质上它们都只是为了表述同一个概念，本文中也会视具体情况交替使用，请读者务必知晓。

2.1.5 本小节小注

以上只是对向量的概念做了一个比较粗略的分类，务必请读者注意：不要割裂来看待它们，因为实际应用中三者的概念往往是相互交叉融合的。

比如向量的定义和证明固然要依靠数学领域来保证其严谨性，但是在涉及大量运算的时候，却往往需要借助计算机的矩阵运算来实现。

2.2 基(Basis)

有了向量的基础，我们先来看看基这个概念。

2.2.1 基的概念

根据维基百科的解释，线性代数意义上的基)（也称为基底）是描述、刻画向量空间的基本工具。

向量空间的基是它的一个特殊的子集，基的元素称为基向量。向量空间中任意一个元素，都可以唯一地表示成基向量的线性组合。

基的本质就是一组（一个或多个）$n(n≥0)$维向量。以二维平面坐标系为例，我们通常会采用向量$\vec i(1, 0)$和$\vec j(0, 1)$作为基，如下图所示：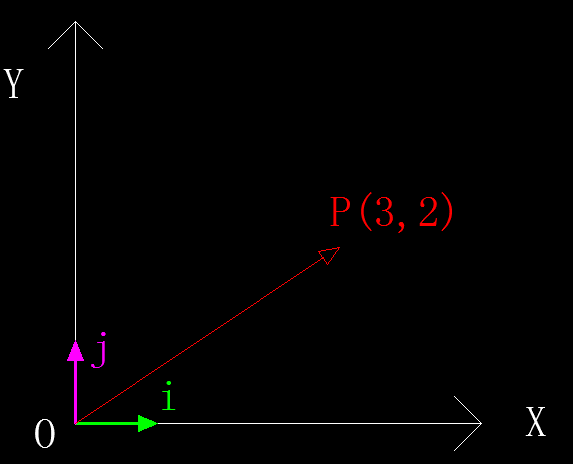

图2-5　　二维平面中的基及向量

定义了基向量后，二维平面坐标系中的其它任意向量都可以表示为这两个基向量的线性组合，比如上图中的向量$\overrightarrow{OP}=(3,2)$，可用基向量表示成：

$$
\overrightarrow{OP}=3\vec i + 2\vec j
$$

上述表达式的含义非常明确，即：

先往$X$(基向量$\vec{i}$)正向移动 3 个单位；
再往$Y$(基向量$\vec{j}$)正向移动 2 个单位。

这也是向量在给定坐标系($XOY$)下坐标值最本质的含义：把向量看做物体的运动。此外还需要注意，基向量可以是任意向量（比如$\vec i=(2,1)$），并不要求必须是单位向量。上面只是举了一个非常特殊的例子（为了方便下文的叙述和证明）。

2.2.2 向量的基变换

正如我在2.2.1中提到的，在二维坐标系中我们通常都会采用$\vec i(1, 0)$和$\vec j(0, 1)$这对向量作为基向量，因为这样简洁、直观，所见即所得（坐标值）。但是有时候我们往往需要以指定的向量（可能是任意值）作为基向量（去表示其它向量），这就涉及到我们要介绍的第一个知识点：向量的基变换。

比如现在要以$\vec a(1, 3)$和$\vec b(-1, 2)$作为基来表示$\overrightarrow{OP}$，如下图所示：

图2-6　　基变换示意图

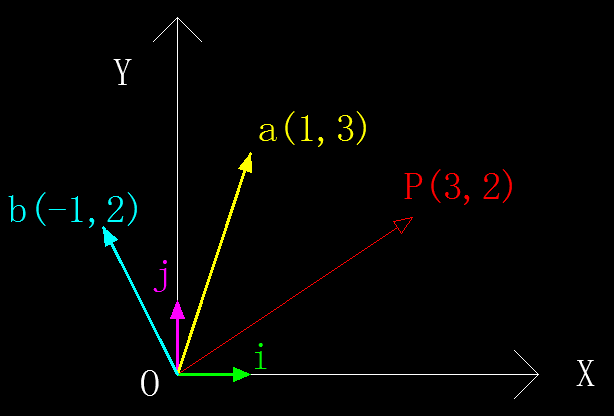
给出了变换后的基向量（下文统一简称新基），如何求解任意向量变换后的新向量呢（下文统一简称新基向量）？

很多教科书上都给出了转换公式，但是并没有一本从几何的角度去解释清楚这个转换的原理和过程。这里推荐英语较好的同学直接去看3Blue1Brown的视频，讲的非常好。

作者在视频中道出了理解和掌握基变换的关键点：变换前后的物体运动的本质（方向、大小）保持不变。

只要牢牢记住这一点，就能清晰的掌握整个变换的脉络。以上面的例子来说，新基为：

$$
\vec{a} = (1,-1), \quad
\vec{b} = (3, \ 2)
$$

不管基如何变换，向量的本质（物体的运动）是不应该改变的，即新基向量$\vec P’$相对于新基的运动也是：

①先沿着基向量$\vec a$移动3个单位（因为变换前的$\vec i$对应变换后的$\vec a$)；
①再沿着基向量$\vec b$移动2个单位。

知道了变换所对应的运动情况，就可以推导出每一步运动后的坐标值，如下：

①沿$\vec a$移动3个单位，即$3\vec a$，到达$P’_a=(0,0) + 3 \times (1,3)=(3,9)$
②再沿$\vec b$移动2个单位，即$2\vec b$，到达终点$P’=P’_a + 2 \times (-1,2)=(1,13)$

变换的详细图解如下所示：

图2-7　　变换后的向量OP’

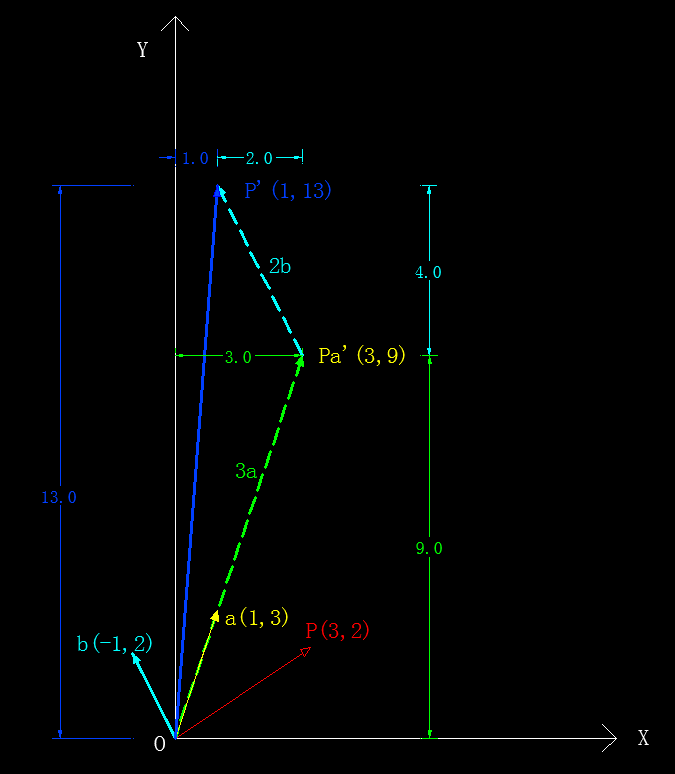
图中蓝色箭头($\vec{OP’}$)即为基变换后的新基向量。根据图中的标注数据可以看出我们利用公式推导出的新基向量的坐标值和实测值（使用AutoCAD2010版自动标注）完全吻合！

其实上述变换还可以进一步细分成四步来看待，即把沿$\vec a$和$\vec b$方向的移动分别拆分成沿X轴和Y轴的移动：

①沿X轴正方向移动3个单位长度($3 \cdot a_x$)，到达点(3,0)；
②沿Y轴正方向移动9个单位长度($3 \cdot a_y$)，到达点(3,9)（这两步相当于完成了沿$\vec a$方向移动3个单位长度）；
③沿X轴负方向移动2个单位长度($2 \cdot b_x$)，到达点(1,9)；
④沿轴Y正方向移动4个单位长度($2 \cdot b_y$)，到达终点(1,13)（这两步相当于完成了沿$\vec b$方向移动2个单位长度）；

2.2.3 向量基变换的矩阵式

上节中虽然推导出了任意向量在基变换后的坐标表达式，但是显然还没有跟线性代数的矩阵和矩阵运算衔接起来。

在上述文字描述计算中，我们也只看到一堆数字在进行运算，并不能清晰、简洁的反映出基向量是如何参与变换的（虽然为了方便读者理解我已经加了不少说明文字），而用矩阵来刻画这个过程则可以很好地解决这些问题。

对于新基的矩阵表达式，因为每一个基向量都是二维（分别对应X、Y坐标值）的，所以该矩阵有两行($m=2$)。又由于有两个基向量（即$\vec a$和$\vec b$），所以矩阵有两列($n=2$)，则新基为$2 \times 2$矩阵，其表达式为：

$$
\vec w =
\begin{bmatrix}
\vec{a}\ \ \vec{b}
\end{bmatrix} =
\begin{bmatrix}
1\ \ -1\\\\
3\ \ \ \ \ \ 2
\end{bmatrix}
\tag{2 - 1}
$$

需要变换的向量$\overrightarrow{OP}$的矩阵表达式则为：

$$
\overrightarrow{OP} =
\begin{bmatrix}
3\\\\
2
\end{bmatrix}
\tag{2 - 2}
$$

根据上文对于基变换的变数可知，新基向量$\overrightarrow{OP’}$的矩阵表达式为：

$$
\begin{split}
\overrightarrow{OP’} =
3·\vec a + 2·\vec b &=
3·\begin{bmatrix}
1\\\\
3
\end{bmatrix} + 2·
\begin{bmatrix}
-1\\\\
2
\end{bmatrix} \\\\
&=
\begin{bmatrix}
1\ \ -1\\\\
3\ \ \ \ \ \ 2
\end{bmatrix} \cdot
\begin{bmatrix}
3\\\\
2
\end{bmatrix} =
\begin{bmatrix}
1\\\\
13
\end{bmatrix} =
\vec w \cdot
\overrightarrow{OP} \\\\
\end{split}
\tag{2 - 3}
$$

由此我们可以得出一个重要结论：新基向量等于要变换的向量左乘新基矩阵。

换个角度来讲，对一个向量左乘一个矩阵，在某些情况下也可以理解为是在进行基变换，但并非所有左乘都是基变换。

这里有非常重要的一点需要强调，要注意将数学运算和几何含义对应起来的充分和必要性。比如，基变换对应的数学运算一定是左乘一个矩阵，但左乘一个矩阵的几何意义却并非一定是基变换。这个道理跟“唐僧骑的一定是白马，但骑白马的却并不一定是唐僧”是一样的。

也就是说，原来以$(\vec i, \ \vec j)$为基，且坐标值为$(3,2)$的点，在新基$(\vec a, \ \vec b)$下的坐标为$(1, 13)$。

更一般的，假设变换后的基、要变换的向量分别为：
$$
\vec w =
\begin{bmatrix}
\vec {i’}\ \ \vec {j’}
\end{bmatrix} =
\begin{bmatrix}
i’_1\ \ i’_2\\\\
j’_1\ \ j’_2
\end{bmatrix}
\ \ ，\ \
\overrightarrow{OP} =
\begin{bmatrix}
x_0\\\\
y_0
\end{bmatrix}
$$
则基变换后的向量为：
$$
\overrightarrow{OP’} =
\underbrace{\begin{bmatrix}
i’_1\ \ i’_2\\\\
j’_1\ \ j’_2
\end{bmatrix}}_{新基矩阵} \cdot
\begin{bmatrix}
x_0\\\\
y_0
\end{bmatrix}
$$

2.3 线性变换

线性变换也称作线性映射，有的书籍把这两个词语作为同义词使用，而有些书籍则不然。这里我们采纳wikipedia词条，其数学定义为：

$$
\begin{cases}
\begin{split}
f(\vec u + \vec v) &= f(\vec u) + f(\vec v) \\\\
f(c\vec u) &=c f(\vec u)
\end{split}
\end{cases}
\tag{2 - 5}
$$

式中$\vec u、\vec v$分别属于$\mathcal{V}、\mathcal{W}$两个向量空间。特别的，当$\mathcal{V} = \mathcal{W}$即两者为同一个向量空间时，我们称之为Linear Operator或者Endomorphism（保留wikipedia上的原话，不做翻译）。

上式也可以整合到一个式子里面，如下所示：

$$
f(m\vec u +n \vec v) = mf(\vec u) + nf(\vec v)
\tag{2 - 6}
$$

它的数学含义是：其运算由两种基本操作即向量加法和标量乘法所组成，并且其数学定义保证了这两种运算的封闭性。
然而，我不是数学专业的学生，也没有成为高斯、欧几里得这类神人的追求（智商），对这些咬文爵字的东西不感兴趣，只喜欢直观的，简单的。

因此对于大多数读者，你只需要记住线性变换的三个特性（敲黑板！！！），以二维向量空间为例：

线性变换前后，坐标系原点保持不动；
线性变换前后，坐标系中任意一条直线必须保持其直线特性，不能被弯曲；
线性变换前后，坐标系中任意两条平行的直线，必须保持其平行特性。

这就是线性变换最简洁、直观的几何特性，只要其中任意一条不满足，都不能称为线性变换。当然，上面三条也可以简化为3Blue1Brown所总结成的一条：变换前后，坐标系中的网格线两两保持等距且平行。

2.3.1 线性变换类型

线性变换其基本形式只有两种：旋转、缩放。从这两种基本变换出发，又可以延伸出诸如投影、镜像、剪切这些变换。

要特别注意的一点是，有一种非常具有迷惑性的变换，它看起来像极了线性变换但却并非线性变换：平移。理由很简单，它不满足上面提到的线性变换几何特性的第一条。

2.3.2 线性变换之缩放

缩放应该是线性变换里面最简单、最容易理解的。这里的缩放特指各方向缩放引子均相同的均匀缩放，它仅仅改变了图形的尺寸大小，但是并没有改变图形的内部结构关系，也没有改变图形与坐标轴的角度关系！

非均匀缩放实际上是一种复合变换，它糅合了均匀缩放和旋转这两种效果。如未特别指明，下文中的缩放均指代均匀缩放。线性变换中的缩放的图示如下：

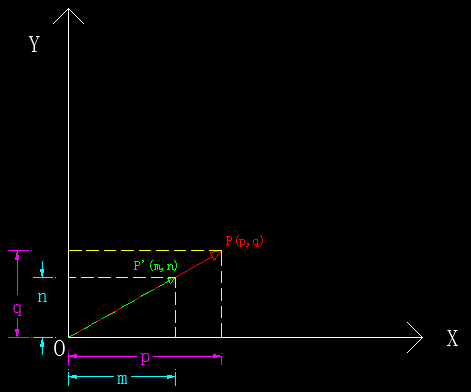图2-8 线性变换之缩放示意图

由图我们有：
$$
\begin{cases}
\frac{m}{p} = \frac{||\vec P_{new}||}{||\vec P_{old}||} \\\\
\frac{n}{q} = \frac{||\vec P_{new}||}{||\vec P_{old}||}
\end{cases}
\tag{2 - 7}
$$
记$\frac {||\vec P_{new}|| } {||\vec P_{old}||} = k$，称为缩放系数，于是我们有：
$$
\begin{cases}
m = k \cdot p + 0 \cdot q \\\\
n = 0 \cdot p + k \cdot q
\end{cases}
\tag{2 - 8}
$$
写成矩阵表达式为：
$$
\begin{bmatrix}
m\ \\\\
n
\end{bmatrix} =
\begin{bmatrix}
k & 0\\\\
0 & k
\end{bmatrix}
\begin{bmatrix}
p \\\\
q
\end{bmatrix}
\tag{2 - 9}
$$
也即缩放前后旧向量和新向量的关系为：
$$
\begin{cases}
\vec P_{old} =
\begin{bmatrix}
\frac{1}{k} & 0\\\\
0 & \frac{1}{k}
\end{bmatrix}
\vec P_{new} = A \cdot \vec P_{new}\\\\
\vec P_{new} =
\begin{bmatrix}
k & 0 \\\\
0 & k
\end{bmatrix}
\vec P_{old} = A^{-1} \cdot \vec P_{old}
\end{cases}
\tag{2 - 10}
$$

由上可知，要均匀缩放一个向量，需要左乘一个主对角线上元素相同的对角矩阵。我们称这个矩阵为缩放矩阵，务必记住缩放矩阵的特性：

主对角元素相等（同值、同号）；
非主对角线上元素均为0（对角矩阵）。

怎么样，够简单吧，那是不是该介绍下一个线性变换了？先别急，这里面要探究的东西还多着。缩放矩阵的非主对角线上的元素为0这一点，我们是从纯数学公式的角度推导出来的，那么单就这一特性，其中所蕴含的几何含义又是什么呢？三维及更高为空间的缩放矩阵又是什么样的？

先来看第一点，要揭开这个谜团其实也很简单。回顾下我们2.2.2小节中讲的向量的基变换，我们把缩放也看做是对已知向量的基变换，那么缩放矩阵即为新基矩阵，新基矩阵与旧基矩阵分别为：

$$
\begin{cases}
\begin{split}
\mathcal{B_{new}} &=
[\vec e_1, \ \vec e_2] &=
\begin{bmatrix}
k & 0 \\
0 & k
\end{bmatrix} \\
\mathcal{B_{old}} &=
[\vec i, \ \vec j] &=
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
\end{split}
\end{cases}
$$

可以看出新基向量分别与旧基向量共线且同向，唯一的差异仅仅只是尺度上有所放大/缩小，比例为$k$。而前面我们提到了，基变换的本质是沿着基向量方向的运动。因此均匀缩放的几何现象就是：图形的方向和角度不会发生改变（因为基向量的方向没有改变），只有尺度上的缩放。

而如果非主对角线上的元素不为0，新基相对于旧基不仅有尺寸上的改变，还有方向（相对于坐标轴的夹角）的改变，用这样的新基去表示一个向量时其对应的运动方向、尺寸也必然同时变化，其最终的变换效果也就不是单纯的缩放了。

再来看第二点。有了上面的知识积累，这个问题也就迎刃而解了。我们仍然把缩放变换视作向量的基变换，要保持向量变换前后只有尺度上的改变，那么变换后的新基向量应该分别与旧基向量方向一致。把握了这一点，对于$n$维坐标系的情况，其缩放矩阵（记为$M_{scale}$）我们也能随手写下来，如下所示：

$$
M_{scale} =
\underbrace{
\begin{bmatrix}
k & 0 & 0 & \cdots & 0 \\\\
0 & k & 0 & \cdots & 0 \\\\
\vdots & \ddots & \ddots & \ddots & \vdots \\\\
0 & 0 & 0 & \cdots & k
\end{bmatrix}
}_{n \times n}
\tag{2 - 11}
$$

2.3.3 线性变换之旋转

我们仍先以二维向量为例，旋转前的向量为$\vec P_{old} = (p, q)$（图中的点P），旋转后的向量$\vec P_{new} = (m, n)$（图中的点P’）。由下图可知，旋转最直观的几何概念就是，只改变了向量（图形）与坐标轴的夹角，而没有改变它的形状。旋转前后向量的情况如下图所示：

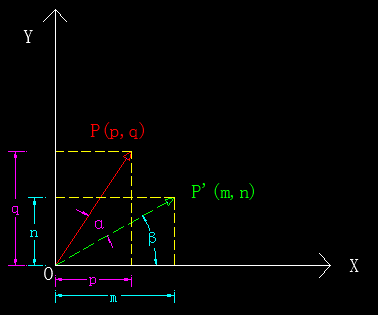图2-9 线性变换之旋转示意图

由图可知，新向量相对于原向量顺时针旋转了$\alpha^°，\alpha \neq 0$，旋转后的新向量与X轴的夹角为$\beta^°$，由图可得到下列方程组：

$$
\begin{split}
\begin{cases}
||\vec P_{old}|| \cdot cos(\alpha + \beta) = p \\\\
||\vec P_{old}|| \cdot sin(\alpha + \beta) = q \\\\
||\vec P_{new}|| \cdot cos(\beta) = m \\\\
||\vec P_{new}|| \cdot sin(\beta) = n \\\\
||\vec P_{old}|| = ||\vec P_{new}||
\end{cases}
\end{split}
\tag{2 - 12}
$$

为方便讨论，我们记$||\vec P_{old}|| = ||\vec P_{new}|| = R$，它表示向量的长度值（二范数），则将上述方程组展开有：

$$
\begin{cases}
R \cdot cos(\alpha)cos(\beta) - R \cdot sin(\alpha)sin(\beta) = p \\\\
R \cdot sin(\alpha)cos(\beta) + R \cdot cos(\alpha)sin(\beta) = q \\\\
R \cdot cos(\beta) = m \\\\
R \cdot sin(\beta) = n \\\\
\end{cases}
\tag{2 - 13}
$$

将上式(2 - 13)的最后两个式子分别代入第一、第二个式子有：

$$
\begin{cases}
p = m \cdot cos(\alpha) - n \cdot sin(\alpha) \\\\
q = m \cdot sin(\alpha) + n \cdot cos(\alpha)\\\\
\end{cases}
\tag{2 - 14}
$$

上式(2 - 14)即为旋转后原向量坐标值关于新向量的坐标值的表达式，写成矩阵的形式如下：

$$
\begin{bmatrix}
p\ \\\\
q
\end{bmatrix} =
\begin{bmatrix}
cos(\alpha)\ \ \ \ \ -sin(\alpha) \\\\
sin(\alpha)\ \ \ \ \ \ cos(\alpha)
\end{bmatrix}
\begin{bmatrix}
m \\\\
n
\end{bmatrix}
\tag{2 - 15}
$$
也即旋转后旧向量和新向量的关系为：
$$
\begin{cases}
\vec P_{old} =
\begin{bmatrix}
cos(\alpha)\ \ \ \ \ -sin(\alpha) \\\\
sin(\alpha)\ \ \ \ \ \ cos(\alpha)
\end{bmatrix}
\vec P_{new} = A \cdot \vec P_{new}\\\\
\vec P_{new} =
\begin{bmatrix}
cos(\alpha)\ \ \ \ \ \ sin(\alpha) \\\\
-sin(\alpha)\ \ \ \ \ cos(\alpha)
\end{bmatrix}
\vec P_{old} = A^{-1} \cdot \vec P_{old}
\end{cases}
\tag{2 - 16}
$$
由上式可知，要旋转一个向量，需要左乘一个关于旋转角度的三角函数矩阵。我们称这个矩阵为旋转矩阵（记为$M_{rotate}$）。

当然，大多数时候旋转矩阵的元素并不会写成三角函数的形式，而是一个普通的实数矩阵。因此我们要记住二维空间中旋转矩阵的特征：

对角线上元素相同，均为旋转角度的余弦值；
处于对称位置的非对角线元素互为相反数，其值为旋转角度的正弦值；
矩阵任意列向量其二范数（长度）必为1；
非对角线元素符号的正负与选取的方向有关（左右手坐标系）。

综上，可给出二维空间中的旋转矩阵的通用形式：

$$
M_{rotate} =
\begin{bmatrix}
\alpha=cos(\theta) & \beta=sin(\theta) \\
-\beta & \alpha
\end{bmatrix}, \quad \sqrt{\alpha^2 + \beta^2} =1, \quad \alpha, \beta \in [-1,1]
\tag{2 - 17}
$$

记住上述三个特性后，给定旋转角度我们就能随手写出二维平面内的旋转矩阵。

同样的，我们仍然利用向量的基变换来分析旋转矩阵。新旧基矩阵分别如下：

$$
\begin{cases}
\begin{split}
\mathcal{B_{new}} &=
[\vec e_1, \ \vec e_2] &=
\begin{bmatrix}
cos(\theta) & sin(\theta) \\
-sin(\theta) & cos(\theta)
\end{bmatrix} \\
\mathcal{B_{old}} &=
[\vec i, \ \vec j] &=
\begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
\end{split}
\end{cases}
\tag{2 - 18}
$$

要分析新旧基向量方向的变化，我们需要借助余弦相似度计算公式来计算，如下：

$$
\begin{cases}
\begin{split}
cos<\vec{e_1}, \vec{i}> = \frac{\vec{e_1} \cdot \vec{i}}{\Vert \vec{e_1} \Vert \cdot \Vert \vec{i} \Vert} = \frac{cos(\theta) \cdot 1 - sin(\theta) \cdot 0}{1 \cdot 1} = cos(\theta) \\
cos<\vec{e_2}, \vec{j}> = \frac{\vec{e_2} \cdot \vec{j}}{\Vert \vec{e_1} \Vert \cdot \Vert \vec{i} \Vert} = \frac{sin(\theta) \cdot 0 + cos(\theta) \cdot 1}{1 \cdot 1} = cos(\theta)
\end{split}
\end{cases}
\tag{2 - 18}
$$

由上式可知变换前后基向量之间的夹角大小都是$\theta$，即基向量做了同步旋转，由此变换后的新向量相对于旧向量整体上也旋转了$\theta$角度。同时由于变换前后运动的绝对距离没有发生改变。

这样有利于我们马上要讲的高维空间的旋转矩阵的求解。三维旋转矩阵推导需要自行脑补的知识点较多，建议作为选读内容。

点此扩展阅读

对于三维空间中的的旋转问题，其旋转矩阵的求解更复杂一些，不过在几何意义上并没有太大的本质区别。

对于三维空间$XYZ$来说，任意一次旋转，我们都可以拆分为在平面$XOY（Yaw角）、XOZ（Pitch角）、YOZ（Roll角）$的旋转的合成（本来复合变换这部分是在本节最后讲的，但这里为了求解高维空间的旋转矩阵，不得不提前讲一些。），并记这三个旋转的角度值为$\alpha、\beta、\gamma$，有了我们刚才讲的旋转矩阵的特性，随手就能写出这三个平面内的旋转矩阵（均为顺时针旋转）来，如下所示：

$$
\begin{cases}
R_{XOY} =
\begin{bmatrix}
cos(\alpha) & -sin(\alpha) &\boxed{\color{blue}0}\\\\
sin(\alpha) & cos(\alpha) &\boxed{\color{blue}0} \\\\
\boxed{\color{blue}0} &\boxed{\color{blue}0} &\boxed{\color{red}1}
\end{bmatrix}
\stackrel{define}{\longrightarrow} Yaw角（绕Z轴）
\\\\
\\\\
R_{XOZ} =
\begin{bmatrix}
cos(\beta) &\boxed{\color{blue}0} &sin(\beta) \\\\
\boxed{\color{blue}0} &\boxed{\color{red}1} &\boxed{\color{blue}0} \\\\
-sin(\beta) &\boxed{\color{blue}0} &cos(\beta)
\end{bmatrix}
\stackrel{define}{\longrightarrow} Pitch角（绕Y轴）
\\\\
\\\\
R_{YOZ} =
\begin{bmatrix}
\boxed{\color{red}1} & \boxed{\color{blue}0} & \boxed{\color{blue}0} \\\\
\boxed{\color{blue}0} & cos(\gamma) & -sin(\gamma) \\\\
\boxed{\color{blue}0} & sin(\gamma) & cos(\gamma)
\end{bmatrix}
\stackrel{define}{\longrightarrow} Roll角（绕X轴）
\end{cases}
\tag{2 - 18 - 1}
$$

注意：wiki词条的三维空间中，右手坐标系以绕Z、X轴的旋转均以逆时针为正，为保持与wiki的一致性，这里我们不再使用上面二维平面中的顺时针旋转为正（左手坐标系）。因此式（2-17）中的第一、三个矩阵中的正弦值符号会有所不同。

只要记住了前面讲的旋转矩阵的特性，这三个矩阵很轻松的就能写出来，只是有两个地方容易弄错。第一个是矩阵中带框的绿色数字部分，第二个是矩阵中带框的蓝色数字部分。以$R_{XOY}$来说，因为是在平面XOY内进行的旋转，所以旋转前后其Z坐标值不会发生变化。因此矩阵中对角线上该坐标轴位置处的系数应该为1（而不是0），而非对角线凡是与不变的坐标轴有关的位置处的系数应该为0（而不是1），至于原因，我们已经在2.3.2小节中讲了。

有了这三个旋转矩阵，我们就可以进行复合（合成）了。这里需要特别注意的是，三个旋转矩阵的复合顺序是有讲究的，因为这三个旋转矩阵都不是对称阵，因此最后的运算结果与矩阵相乘的顺序严格相关。对这一现象的解释就是，我们仍然把每一次旋转当做向量的基变换，每一次基变换都是基于前一次操作后的新基的，而每一次旋转后，基向量的坐标值、方向已经发生了改变（而不再是原本的$[\vec i, \vec j]^T$）。

按照Z-Y-X（这里我们采用Z-Y-X旋转顺序的Tait-Bryan角）的旋转顺序，我们的旋转矩阵作用的先后顺序及作用结果如下：

$$
\begin{split}
\vec P_{new} &= \underbrace{ R_{XOY}
\underbrace{ (R_{XOZ}
\underbrace{ (R_{YOZ} \vec P_{old}) } _{绕X轴旋转}
} _{绕Y轴旋转}) } _{绕Z轴旋转} \\\\
&= (R_{XOY} R_{XOZ} R_{YOZ}) \vec P_{old} \\\\
&=
\begin{bmatrix}
cos(\alpha) cos(\beta) & - sin(\alpha) cos(\gamma) + cos(\alpha) sin(\beta) sin(\gamma) & sin(\alpha) sin(\gamma) + cos(\alpha) sin(\beta) cos(\gamma) \\\\
sin(\alpha) cos(\beta) & cos(\alpha) cos(\beta) + sin(\alpha)sin(\beta) sin(\gamma) & -cos(\alpha)sin(\gamma) + sin(\alpha) sin(\beta) cos(\gamma) \\\\
-sin(\beta) & cos(\beta)sin(\gamma) & cos(\beta) cos(\gamma) \\\\
\end{bmatrix}
\vec P_{old}
\end{split}
\tag{2 - 18 -2}
$$

注意：不同的旋转顺序所计算出来的最终旋转矩阵会完全不同，这里仅做演示用，并非唯一结果。

至于四维及以上空间，去讨论其几何意义已经是不可能也不具备实际价值的了（反正我是想象不出四维空间长什么样）。其旋转矩阵资料参见Givens rotation。本部分选读内容由于涉及的知识点太多，这里就不深入去探讨了，写这部分的目的也仅仅是为了方便理解我们后面要讲的内容，感兴趣的请自行查阅相关资料。

附上本小节所参考的一些网络资料如下：
- 1. 旋转矩阵与四元数;
- 2. Yaw, pitch, and roll rotations;
- 3. Three-dimensional rotation operator;
- 4. Rotation matrix;
- 5. 3D图形:矩阵与线性变换;

作为线性变换的基本操作之一，掌握旋转矩阵的特性将有助于我们去理解更复杂的内容。

2.3.4 线性变换之非均匀缩放

非均匀缩放属于复合的线性变换，它融合了线性变换的两大基础变换：均匀缩放和旋转。同样以二维向量为例，记变换前向量为$\vec{OP} = (p, q), \ p \neq 0, q \neq 0$，变换后向量为$\vec{OP}’ = (m, n)$，X、Y轴方向上的缩放因子分别为：$k_x、k_y$，且$k_x \neq k_y$，则有：

$$
\begin{cases}
\begin{split}
k_x &= \frac{m}{p} \\
k_y &= \frac{n}{q}
\end{split}
\end{cases}
$$

3. 后记

3.1 结语

本系列才开了个头就写结语似乎有点怪怪的，但我觉得有必要这样。看到各位的留言，实在惭愧。因为平时工作较忙，博客这边就有点力不从心，不过请各位放心，我一定把本系列写好、写完。你们的批评和支持将是我最诚挚的动力！

3.1 修改记录

1. 2018-03-04 修改2.2.2节的标题“基变换”为“向量的基变换”，原标题可能会误导读者，线性代数中的基变换更侧重于两组不同的基之间如何进行转换，涉及到过渡矩阵，而我在这节中讲的则更侧重于给定坐标系中任意向量在新、旧基之间转换时如何计算。
2. 2018-03-04 修改2.2.3节的标题“基变换的矩阵式”为“向量基变换的矩阵式”，原因同上。
3. 2019-05-19 重新排版，修改相应的内容。